
【題目】如圖,某城市有一條公路正西方AO通過市中心O后轉向北偏東α角方向的OB,位于該市的某大學M與市中心O的距離OM=3 ![]() km,且∠AOM=β,現要修筑一條鐵路L,L在OA上設一站A,在OB上設一站B,鐵路在AB部分為直線段,且經過大學M,其中tanα=2,cosβ=
km,且∠AOM=β,現要修筑一條鐵路L,L在OA上設一站A,在OB上設一站B,鐵路在AB部分為直線段,且經過大學M,其中tanα=2,cosβ= ![]() ,AO=15km.
,AO=15km. 
(1)求大學M在站A的距離AM;
(2)求鐵路AB段的長AB.
【答案】
(1)解:在△AOM中,A0=15,∠AOM=β,且cosβ= ![]() ,OM=3
,OM=3 ![]() ,
,
由余弦定理可得:AM2=OA2+OM2﹣2OAOMcos∠AOM=(3 ![]() )2+152﹣2×3
)2+152﹣2×3 ![]() ×15×
×15× ![]() =72.
=72.
所以可得:AM=6 ![]() ,大學M在站A的距離AM為6
,大學M在站A的距離AM為6 ![]() km
km
(2)解:∵cos ![]() ,且β為銳角,∴sinβ=
,且β為銳角,∴sinβ= ![]() ,
,
在△AOM中,由正弦定理可得: ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,∴sin∠MAO=
,∴sin∠MAO= ![]() ,
,
∴∠MAO= ![]() ,∴∠ABO=α﹣
,∴∠ABO=α﹣ ![]() ,
,
∵tanα=2,∴sin ![]() ,cosα=
,cosα= ![]() ,
,
∴sin∠ABO=sin( ![]() )=
)= ![]() ,
,
又∵∠AOB=π﹣α,∴sin∠AOB=sin(π﹣α)= ![]() .
.
在△AOB中,AO=15,由正弦定理可得: ![]() =
= ![]() ,即
,即 ![]() ,∴解得AB=30
,∴解得AB=30 ![]() ,即鐵路AB段的長AB為30
,即鐵路AB段的長AB為30 ![]() km
km
【解析】(1)在△AOM中,利用已知及余弦定理即可解得AM的值;(2)由cos ![]() ,且β為銳角,可求sinβ,由正弦定理可得sin∠MAO,結合tanα=2,可求sinα,cosα,sin∠ABO,sin∠AOB,結合AO=15,由正弦定理即可解得AB的值.
,且β為銳角,可求sinβ,由正弦定理可得sin∠MAO,結合tanα=2,可求sinα,cosα,sin∠ABO,sin∠AOB,結合AO=15,由正弦定理即可解得AB的值.
【考點精析】掌握正弦定理的定義是解答本題的根本,需要知道正弦定理:![]() .
.


科目:高中數學 來源: 題型:
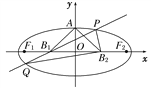
【題目】已知動點M(x,y)到直線l:x=4的距離是它到點N(1,0)的距離的2倍.
(1)求動點M的軌跡C的方程;
(2)過點P(0,3)的直線m與軌跡C交于A,B兩點,若A是PB的中點,求直線m的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是( )
=0.85x-85.71,則下列結論中不正確的是( )
A. y與x具有正的線性相關關系
B. 若給變量x一個值,由回歸直線方程![]() =0.85x-85.71得到一個
=0.85x-85.71得到一個![]() ,則
,則![]() 為該統計量中的估計值
為該統計量中的估計值
C. 若該大學某女生身高增加1 cm,則其體重約增加0.85 kg
D. 若該大學某女生身高為170 cm,則可斷定其體重必為58.79 kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() ,數列
,數列![]() 滿足
滿足![]() 點
點![]() 在直線
在直線![]() 上.
上.
(1)求數列![]() ,
, ![]() 的通項
的通項![]() ,
, ![]() ;
;
(2)令![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,求對所有的正整數
,求對所有的正整數![]() 都有
都有![]() 成立的
成立的![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一袋中裝有6個黑球,4個白球.如果不放回地依次取出2個球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的條件下,第2次又取到黑球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,ABCD﹣A1B1C1D1是棱長為a的正方體,M、N分別是下底面的棱A1B1 , B1C1的中點,P是上底面的棱AD上的一點,AP= ![]() ,過P、M、N的平面交上底面于PQ,Q在CD上,則PQ= .
,過P、M、N的平面交上底面于PQ,Q在CD上,則PQ= . 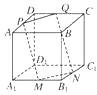
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為非零常數.
為非零常數.
(1)若![]() ,
, ![]() ,求證:
,求證: ![]() 為等比數列,并求數列
為等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 是公差不等于零的等差數列.
是公差不等于零的等差數列.
①求實數![]() ,
, ![]() 的值;
的值;
②數列![]() 的前
的前![]() 項和
項和![]() 構成數列
構成數列![]() ,從
,從![]() 中取不同的四項按從小到大排列組成四項子數列.試問:是否存在首項為
中取不同的四項按從小到大排列組成四項子數列.試問:是否存在首項為![]() 的四項子數列,使得該子數列中的所有項之和恰好為2017?若存在,求出所有滿足條件的四項子數列;若不存在,請說明理由.
的四項子數列,使得該子數列中的所有項之和恰好為2017?若存在,求出所有滿足條件的四項子數列;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點A是以線段BC為直徑的圓O上一點,AD⊥BC于點D,過點B作圓O的切線,與CA的延長線相交于點E,點G是AD的中點,連接CG并延長與BE相交于點F,延長AF與CB的延長線相交于點P. 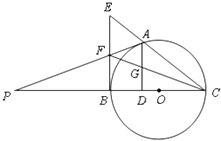
(1)求證:BF=EF;
(2)求證:PA是圓O的切線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com