(0,2]

3
分析:A、根據絕對值的幾何意義,我們易分析出|x+3|-|x+2|表示數軸上的x到-2和-3的距離之和,求出|x+3|-|x+2|的最小值后,即可得到實數a的取值范圍.
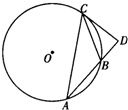
B、利用割線定理我們易求出PA、PB、PC、PD的比例,由圓外接四邊形定理,我們易判斷出△PBC∽△PDA,根據相似三角形對應邊成比例,我們易得到答案.
C、根據已知中曲線和直線的極坐標方程,我們易求出圓的標準方程和直線的一般方程,判斷出直線與圓的位置關系,即可得到結論.
解答:A∵關于x的不等式|x+3|-|x+2|≥log
2a有解,
|x+3|-|x+2|表示數軸上的x到-3和-2的距離之差,其最小值等于-1,最大值是1,
由題意log
2a≤1,
∴0<a≤2.
故答案為:(0,2]
B、∵
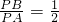
,
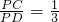
,
∴設 PB=m,PC=n,則 PA=2 m,PD=3n,
由切割線定理得:PA•PB=PC•PD
即2m
2=3n
2故m:n=

:

由圓外接四邊形定理得:∠PBC=∠PDA,∠PCB=∠PAD
∴△PBC∽△PDA
∴
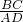
=
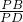
=

=

故答案為:

C、∵曲線C的參數方程為
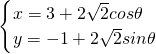
(θ為參數),
∴曲線C的標準方程這:(x-3)
2+(y+1)
2=8,它表示以(3,-1)點為圓心,以2

為半徑的圓
又∵直線l的極坐標方程為
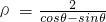
,
∴它的一般方程為x-y-2=0
∵(3,-1)點到直線x-y-2=0的距離為

,等于圓半徑的一半
故曲線C上到直線l距離為

的點的個數為3個
故答案為:3
點評:本題考查的知識點是簡單曲線的極坐標方程,與圓有關的比例線段,絕對不等式的解法,A中關鍵是掌握絕對值的幾何意義,B中關系是求出PA、PB、PC、PD的比例,C中的關鍵是求出圓的標準方程和直線的一般方程.

 A.(不等式選做題)若關于x的不等式|x+3|-|x+2|≥log2a有解,則實數a的取值范圍是:________.
A.(不等式選做題)若關于x的不等式|x+3|-|x+2|≥log2a有解,則實數a的取值范圍是:________.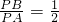 ,
,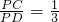 ,則
,則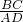 的值為________.
的值為________.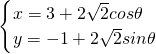 (θ為參數),以原點為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為
(θ為參數),以原點為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為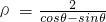 ,則曲線C上到直線l距離為
,則曲線C上到直線l距離為 的點的個數為:________.
的點的個數為:________. 3
3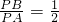 ,
,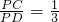 ,
, :
:
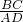 =
=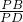 =
= =
=

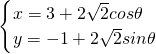 (θ為參數),
(θ為參數), 為半徑的圓
為半徑的圓 ,
, ,等于圓半徑的一半
,等于圓半徑的一半 的點的個數為3個
的點的個數為3個

 A.(不等式選做題)
A.(不等式選做題)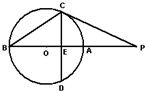 A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為
A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為
 (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分) 選做題:(考生注意:請在下列三題中任選一題作答,如果多做,則按所做第一題評分)
選做題:(考生注意:請在下列三題中任選一題作答,如果多做,則按所做第一題評分)