
���}Ŀ���^(gu��)�E�A![]() ��
�� ![]() ��һ�c(di��n)
��һ�c(di��n)![]() ��
��![]() �S������(xi��n)��������ҽ��c(di��n)
�S������(xi��n)��������ҽ��c(di��n)![]() ��
�� ![]() ��
��![]() �քe��E�A
�քe��E�A![]() ������c(di��n)������c(di��n)����
������c(di��n)������c(di��n)����![]() ��
�� ![]() .
.
������E�A![]() �ķ��̣�
�ķ��̣�
�������(d��ng)ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��ֱ���ĈA���^(gu��)����(bi��o)ԭ�c(di��n)
��ֱ���ĈA���^(gu��)����(bi��o)ԭ�c(di��n)![]() .��(w��n)�Ƿ����һ��(g��)���A�c��(d��ng)ֱ��(xi��n)
.��(w��n)�Ƿ����һ��(g��)���A�c��(d��ng)ֱ��(xi��n)![]() ������.�����ڣ����ԓ���A�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
������.�����ڣ����ԓ���A�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
���𰸡���1��![]() ��2������
��2������
��������ԇ�}��������1����![]() ��
��![]() �����
�����![]() ��
�� ![]() �����Y(ji��)��
�����Y(ji��)��![]() ��������E�A
��������E�A![]() �ķ��̣���2�������ֱ��(xi��n)
�ķ��̣���2�������ֱ��(xi��n)![]() ��б�ʲ����ڼ�б�ʞ���r(sh��)�A�ķ��̣��ɴ˿ɵÃɈA���^(gu��)�����c(di��n)��ԭ�c(di��n)
��б�ʲ����ڼ�б�ʞ���r(sh��)�A�ķ��̣��ɴ˿ɵÃɈA���^(gu��)�����c(di��n)��ԭ�c(di��n)![]() ����(d��ng)ֱ��(xi��n)
����(d��ng)ֱ��(xi��n)![]() ��б�ʴ����Ҳ�����r(sh��)���O(sh��)ֱ��(xi��n)
��б�ʴ����Ҳ�����r(sh��)���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ����E�A��������
����E�A��������![]() ��
��![]() �Ķ��η��̣��O(sh��)
�Ķ��η��̣��O(sh��)![]() �����f�_(d��)������������(sh��)���e�ɵ�
�����f�_(d��)������������(sh��)���e�ɵ�![]() �ı��_(d��)ʽ���ٸ���(j��)��(xi��n)�A���пɵ�
�ı��_(d��)ʽ���ٸ���(j��)��(xi��n)�A���пɵ�![]() ���P(gu��n)ϵʽ�������������_(d��)ʽ�����
���P(gu��n)ϵʽ�������������_(d��)ʽ�����![]() ���ɴ˿ɵýY(ji��)Փ.
���ɴ˿ɵýY(ji��)Փ.
ԇ�}��������1�����}���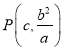 ������
������![]() ��
�� ![]() .��
.��![]() ��
��![]() �����
�����![]() ��
�� ![]() ��
��
��![]() ����
����![]() ��
�� ![]() ���E�A
���E�A![]() �ķ��̞�
�ķ��̞�![]() .
.
��2�����O(sh��)�����@�ӵĈA.�O(sh��)![]() ��
�� ![]() .
.
����֪����![]() ��ֱ���ĈA���^(gu��)ԭ�c(di��n)
��ֱ���ĈA���^(gu��)ԭ�c(di��n)![]() ����
����![]() ������
������![]() .
.
��(d��ng)ֱ��(xi��n)![]() ��ֱ��
��ֱ��![]() �S�r(sh��)��
�S�r(sh��)�� ![]() ��
�� ![]() ������
������![]() ����
����![]() �����
�����![]() ��
��
�����O(sh��)![]() ��
�� ![]() ��
��![]() ��
�� ![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ���˕r(sh��)ԭ�c(di��n)
���˕r(sh��)ԭ�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x��
�ľ��x��![]() .
.
��(d��ng)ֱ��(xi��n)![]() ��б�ʴ��ڕr(sh��)�����O(sh��)ֱ��(xi��n)
��б�ʴ��ڕr(sh��)�����O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ����
����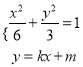 ��ȥ
��ȥ![]() �÷��̣�
�÷��̣�
![]()
![]() ����?y��n)�ֱ��(xi��n)
����?y��n)�ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() ����
����![]() ��
�� ![]() ���c(di��n)�����Է��̵��Єeʽ
���c(di��n)�����Է��̵��Єeʽ
![]()
![]() ����
����![]() ����
����![]() ��
�� ![]() .
.
��![]() ����
����![]()
![]() ��
��
����![]()
![]() ��������
��������![]() ���M(m��n)��
���M(m��n)��![]() ��.
��.
����ԭ�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x
�ľ��x![]() .�C��������ԭ�c(di��n)
.�C��������ԭ�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x�鶨ֵ
�ľ��x�鶨ֵ![]() �������ڶ��A
�������ڶ��A![]() ���cֱ��(xi��n)
���cֱ��(xi��n)![]() ����.
����.


 ���ل�(chu��ng)���������W(xu��)��(x��)�����W(xu��)�ں���㕽�ϵ�д�
���ل�(chu��ng)���������W(xu��)��(x��)�����W(xu��)�ں���㕽�ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M(m��n)��10�֣�
��֪���µ�ʽ�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��(d��ng)![]() �r(sh��)��ԇ����
�r(sh��)��ԇ����![]() ��ֵ�����Ô�(sh��)�W(xu��)�w�{���o���C����
��ֵ�����Ô�(sh��)�W(xu��)�w�{���o���C����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij��λ���x��(w��)�I(xi��n)Ѫ�����w�z�ϸ�����У� ![]() ��Ѫ�Ĺ���28�ˣ�
��Ѫ�Ĺ���28�ˣ� ![]() ��Ѫ�Ĺ���7�ˣ�
��Ѫ�Ĺ���7�ˣ� ![]() ��Ѫ�Ĺ���9�ˣ�
��Ѫ�Ĺ���9�ˣ� ![]() ��Ѫ����3�ˣ�
��Ѫ����3�ˣ�
��1���������x1��ȥ�I(xi��n)Ѫ���ж��ٷN��ͬ���x����
��2�����ķNѪ�͵����и��x1��ȥ�I(xi��n)Ѫ���ж��ٷN��ͬ���x����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���� ![]() =��cos��x��sin��x����
=��cos��x��sin��x���� ![]() =��cos��x��
=��cos��x�� ![]() cos��x�������Цأ�0���O(sh��)����(sh��)f��x��=
cos��x�������Цأ�0���O(sh��)����(sh��)f��x��= ![]()
![]() ��
��
��1��������(sh��)f��x������С�������ǦУ���(sh��)f��x���Ć��{(di��o)�f���^(q��)�g��
��2��������(sh��)f��x���ĈD���һ��(g��)��(du��)�Q(ch��ng)���ĵęM����(bi��o)�� ![]() ����ص���Сֵ��
����ص���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪f��x��=2![]() sinxcosx+2cos2x��1��
sinxcosx+2cos2x��1��
��1����f��x�������ֵ���Լ�ԓ����(sh��)ȡ���ֵ�r(sh��)x��ȡֵ���ϣ�
��2���ڡ�ABC�У�a��b��c�քe�ǽ�A��B��C����(du��)��߅�L(zh��ng)����![]() �����C��
�����C��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]()
����������(sh��)![]() ��
��![]() ̎���о�(xi��n)�cֱ��(xi��n)
̎���о�(xi��n)�cֱ��(xi��n)![]() ��ֱ����
��ֱ����![]() ��ֵ��
��ֵ��
����ӑՓ����(sh��)![]() �Oֵ�c(di��n)�Ă�(g��)��(sh��)�����f(shu��)�����ɣ�
�Oֵ�c(di��n)�Ă�(g��)��(sh��)�����f(shu��)�����ɣ�
������![]() ��
�� ![]() ���������
���������![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������ijУ�����꼉(j��)�W(xu��)�������˔�(sh��)�W(xu��)�y(c��)ԇ���겿�M�����n�̎���(du��)�@�ο�ԇ�M(j��n)�гɿ�(j��)����.�F(xi��n)���г�ȡ80���W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ�(j��)����������(sh��)�����l�ʷֲ�ֱ���D��D��ʾ.
����Ӌ(j��)�@���¿���(sh��)�W(xu��)�ɿ�(j��)��ƽ���ֺͱ���(sh��)��
�����O(sh��)����W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ�(j��)?c��)?/span>![]() �θ�����ͬ���Ҷ����^(gu��)94��.���l��ҕ����ʣ��F(xi��n)�ú�(ji��n)���S�C(j��)��ӵķ�������95��96��97��98��99��100�@6��(g��)��(sh��)���������ȡ2��(g��)��(sh��)���зŻصس�ȡ3�Σ�ӛ�@3�γ�ȡ��ǡ���Ѓ����W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ�(j��)�ĴΔ�(sh��)��
�θ�����ͬ���Ҷ����^(gu��)94��.���l��ҕ����ʣ��F(xi��n)�ú�(ji��n)���S�C(j��)��ӵķ�������95��96��97��98��99��100�@6��(g��)��(sh��)���������ȡ2��(g��)��(sh��)���зŻصس�ȡ3�Σ�ӛ�@3�γ�ȡ��ǡ���Ѓ����W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ�(j��)�ĴΔ�(sh��)��![]() ����
����![]() �ķֲ��к�����.
�ķֲ��к�����.
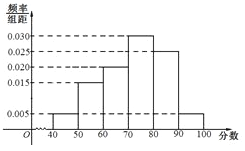
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����2015�߿���������D���AC�cx�S�������c(di��n)T(1��0)���cy�S�����S���ڃ��c(di��n)A��B(B��A���Ϸ�)����|AB|��2.
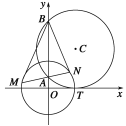
(1)�AC�Ę�(bi��o)��(zh��n)���̞�_(k��i)_______��
(2)�^(gu��)�c(di��n)A����һ�lֱ��(xi��n)�c�AO��x2��y2��1�ཻ��M��N���c(di��n)����������(g��)�Y(ji��)Փ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��2��
��2��
��![]() ��
��![]() ��2
��2![]() .
.
�������_�Y(ji��)Փ����̖(h��o)��________(��(xi��)���������_�Y(ji��)Փ����̖(h��o))��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������w![]() �У�
�У� ![]() �քe��
�քe��![]() �����c(di��n).
�����c(di��n).
��1���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ
��ʹ![]() ƽ��
ƽ��![]() ��Ո(q��ng)�C����ĽY(ji��)Փ.
��Ո(q��ng)�C����ĽY(ji��)Փ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com