
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等邊三角形,四邊形ABCD是矩形,
是等邊三角形,四邊形ABCD是矩形,![]() ,F為棱PA上一點,且
,F為棱PA上一點,且![]() ,M為AD的中點,四棱錐
,M為AD的中點,四棱錐![]() 的體積為
的體積為![]() .
.
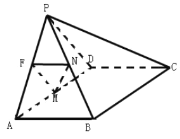
(1)若![]() ,N是PB的中點,求證:平面
,N是PB的中點,求證:平面![]() 平面PCD;
平面PCD;
(2)是否存在![]() ,使得平面FMB與平面PAD所成的二面角余弦的絕對值為
,使得平面FMB與平面PAD所成的二面角余弦的絕對值為![]() .
.
【答案】(1)詳見解析(2)存在![]() ,使得平面FMB與平面PAD所成的二面角余弦的絕對值為
,使得平面FMB與平面PAD所成的二面角余弦的絕對值為![]()
【解析】
(1)由已知有![]() ,
,![]() ,即可證明
,即可證明![]() 平面PCD;
平面PCD;
(2)建立以M為原點,MA為x軸,ME為y軸,MP為z軸建立空間直角坐標系![]() ,則可得FMN的法向量為
,則可得FMN的法向量為![]() ,取面PAD的法向量
,取面PAD的法向量![]() ,由向量的數量積公式計算可得解.
,由向量的數量積公式計算可得解.
解:(1)因為![]() ,所以F是AP的中點,又因為N是PB的中點,所以
,所以F是AP的中點,又因為N是PB的中點,所以![]() ,由四邊形ABCD是矩形,得
,由四邊形ABCD是矩形,得![]() ,故
,故![]() ,
,


 ;
;
(2)連接PM,過M作![]() 交BC于E,由
交BC于E,由![]() 是等邊三角形,得
是等邊三角形,得![]() ,
, ,以M為原點,MA為x軸,ME為y軸,MP為z軸建立空間直角坐標系
,以M為原點,MA為x軸,ME為y軸,MP為z軸建立空間直角坐標系![]() ,
,

假設存在![]() ,滿足題意,設
,滿足題意,設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
設面FMN的法向量為![]() ,所以
,所以 ,
,
取![]() ,得
,得![]() ,取面PAD的法向量
,取面PAD的法向量![]() ,
,
由題知: ,解得
,解得![]() ,
,
所以,存在![]() ,使得平面FMB與平面PAD所成的二面角余弦的絕對值為
,使得平面FMB與平面PAD所成的二面角余弦的絕對值為![]()


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為π,它的一個對稱中心為(
的最小正周期為π,它的一個對稱中心為(![]() ,0)
,0)
(1)求函數y=f(x)圖象的對稱軸方程;
(2)若方程f(x)=![]() 在(0,π)上的解為x1,x2,求cos(x1-x2)的值.
在(0,π)上的解為x1,x2,求cos(x1-x2)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】檳榔原產于馬來西亞,中國主要分布在云南、海南及臺灣等熱帶地區,在亞洲熱帶地區廣泛栽培.檳榔是重要的中藥材,在南方一些少數民族還有將果實作為一種咀嚼嗜好品,但其被世界衛生組織國際癌癥研究機構列為致癌物清單Ⅰ類致癌物.云南某民族中學為了解![]() ,
,![]() 兩個少數民族班學生咀嚼檳榔的情況,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周咀嚼檳榔的顆數作為樣本繪制成莖葉圖如圖所示(圖中的莖表示十位數字,葉表示個位數字).
兩個少數民族班學生咀嚼檳榔的情況,分別從這兩個班中隨機抽取5名同學進行調查,將他們平均每周咀嚼檳榔的顆數作為樣本繪制成莖葉圖如圖所示(圖中的莖表示十位數字,葉表示個位數字).
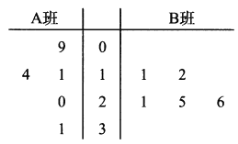
(1)從![]() 班的樣本數據中隨機抽取一個不超過19的數據記為
班的樣本數據中隨機抽取一個不超過19的數據記為![]() ,從
,從![]() 班的樣本數據中隨機抽取一個不超過21的數據記為
班的樣本數據中隨機抽取一個不超過21的數據記為![]() ,求
,求![]() 的概率;
的概率;
(2)從所有咀嚼檳榔顆數在20顆以上(包含20顆)的同學中隨機抽取3人,求被抽到![]() 班同學人數的分布列和數學期望.
班同學人數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是( )
A.“![]() ”是“直線
”是“直線![]() 與直線
與直線![]() 相互平行”的充分不必條件
相互平行”的充分不必條件
B.“直線![]() 垂直平面
垂直平面![]() 內無數條直線”是“直線
內無數條直線”是“直線![]() 垂直于平面
垂直于平面![]() ”的充分條件
”的充分條件
C.已知![]() 、
、![]() 、
、![]() 為非零向量,則“
為非零向量,則“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
D.![]() :存在
:存在![]() ,
,![]() .則
.則![]() :任意
:任意![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2016年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組,得到的頻率分布表如下表所示.
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 | 0.050 |
第2組 |
| n | 0.350 |
第3組 |
| 30 | p |
第4組 |
| 20 | 0.200 |
第5組 |
| 10 | 0.100 |
合計 | 100 | 1.000 |
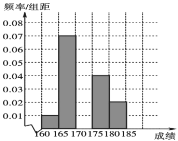
(1)求頻率分布表中n,p的值,并估計該組數據的中位數(保留l位小數);
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試,則第3、4、5組每組各抽取多少名學生進入第二輪面試?
(3)在(2)的前提下,學校決定從6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有1名學生被甲考官面試的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】斐波那契數列,又稱黃金分割數列.因數學家列昂納多·斐波那契以兔子繁殖為例子而引入,故又稱為“兔子數列”,指的是這樣一個數列:1、1、2、3、5、8、13、21、34、…..,在數學上,斐波那契數列以如下被遞推的方法定義:![]() ,
,![]() ,
,![]() .這種遞推方法適合研究生活中很多問題.比如:一六八中學食堂一樓到二樓有15個臺階,某同學一步可以跨一個或者兩個臺階,則他到二樓就餐有( )種上樓方法.
.這種遞推方法適合研究生活中很多問題.比如:一六八中學食堂一樓到二樓有15個臺階,某同學一步可以跨一個或者兩個臺階,則他到二樓就餐有( )種上樓方法.
A.377B.610C.987D.1597
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發現這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com