【題目】已知向量 
， 
滿足| |= 
，| |=1，且對任意實數x，不等式| +x |≥| + |恒成立，設 與 的夾角為θ，則tan2θ=（ ）
A.﹣ 
B.
C.﹣ 
D.
【答案】D
【解析】解：由平面向量加法的幾何意義，只有當（ 
） 
時，對于任意實數x，不等式| 
+x 
|≥| + |恒成立，如圖所示，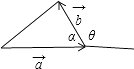 
設 
或 
，
斜邊大于直角邊恒成立，
則不等式| +x |≥| + |恒成立，
∵向量 ， 滿足| |= 
，| |=1，
∴tanθ=﹣2，
∴tan2θ= 
．
故選：D．
另：將不等式| +x |≥| + |兩邊平方得到不等式| +x |2≥| + |2 ， 展開整理得得， 
恒成立，
所以判別式 
，解得cosθ= 
，sinθ= 
，所以tanθ=﹣2，tan2θ= 
；
故選D．
【考點精析】通過靈活運用數量積表示兩個向量的夾角，掌握設
、
都是非零向量，
，
，
是與
的夾角，則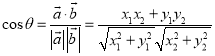
即可以解答此題．
百年學典課時學練測系列答案科目：高中數學 來源： 題型：
【題目】定義在R上的偶函數f（x）滿足f（x+1）= 
，且f（x）在[﹣3，﹣2]上是減函數，若α，β是銳角三角形的兩個內角，則（ ）
A.f（sinα）＞f（sinβ）
B.f（cosα）＞f（cosβ）
C.f（sinα）＞f（cosβ）
D.f（sinα）＜f（cosβ）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn ． 已知a1=1， 
=an+1﹣ 
n2﹣n﹣ 
，n∈N* ．
（1）求數列{an}的通項公式；
（2）設數列{bn}滿足an﹣an﹣1=bna 
，求數列{bn}的n前項和Tn；
（3）是否存在實數λ，使得不等式λa 
﹣ 
+a + 
≥0恒成立，若存在，求出λ的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的短軸長為
，右焦點為
，點
是橢圓
上異于左、右頂點
的一點．
（1）求橢圓
的方程；
（2）若直線
與直線
交于點
，線段
的中點為
，證明：點
關于直線
的對稱點在直線
上．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2cos（ωx+ 
）（其中ω＞0，x∈R）的最小正周期為10π．
（1）求ω的值；
（2）設α，β∈[0， 
]，f（5α+ 
）=﹣ 
，f（5β﹣ 
）= 
，求cos（α+β）的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=x2+ax+3．
（1）當x∈R時，f（x）≥a恒成立，求a的取值范圍．
（2）當x∈[﹣2，2]時，f（x）≥a恒成立，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列判斷：
①從個體編號為1，2，…，1000的總體中抽取一個容量為50的樣本，若采用系統抽樣方法進行抽取，則分段間隔應為20；
②已知某種彩票的中獎概率為 
，那么買1000張這種彩票就一定會中獎（假設該彩票有足夠的張數）；
③從裝有2個紅球和2個黒球的口袋內任取2個球，恰有1個黒球與恰有2個黒球是互斥但不對立的兩個事件；
④設具有線性相關關系的變量的一組數據是（1，3），（2，5），（3，6），（6，8），則它們的回歸直線一定過點（3， 
）．
其中正確的序號是（ ）
A.①、②、③
B.①、③、④
C.③、④
D.①、③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=x2﹣ax+a（x∈R）同時滿足：
①不等式f（x）≤0的解集有且只有一個元素；
②在定義域內存在0＜x1＜x2 ， 使得不等式f（x1）＞f（x2）成立．設數列{an}的前n項和Sn=f（n）．
（1）求f（x）的表達式；
（2）求數列{an}的通項公式；
（3）設 
，cn= 
，{cn}的前n項和為Tn ， 若Tn＞2n+t對任意n∈N，n≥2恒成立，求實數t的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
