
【題目】閱讀下列有關光線的入射與反射的兩個事實現象:現象(1):光線經平面鏡反射滿足入射角與反射角相等(如圖);現象(2);光線從橢圓的一個焦點出發經橢圓反射后通過另一個焦點(如圖).試結合,上述事實現象完成下列問題:
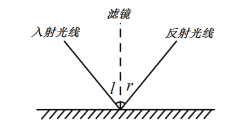
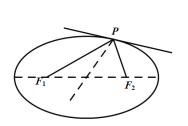
(Ⅰ)有一橢圓型臺球桌,長軸長為2a,短軸長為2b.將一放置于焦點處的桌球擊出.經過球桌邊緣的反射(假設球的反射充全符合現象(2)),后第一次返回到該焦點時所經過的路程記為S,求S的值(用a,b表示);
(Ⅱ)結論:橢圓![]() 上任點P(x0,y0)處的切線的方程為
上任點P(x0,y0)處的切線的方程為![]() .記橢圓C的方程為C:
.記橢圓C的方程為C:![]() ,在直線x=4上任一點M向橢圓C引切線,切點分別為A,B.求證:直線lAB恒過定點:
,在直線x=4上任一點M向橢圓C引切線,切點分別為A,B.求證:直線lAB恒過定點:
(Ⅲ)過點T(1,0)的直線l(直線l斜率不為0)與橢圓C:![]() 交于P、Q兩點,是否存在定點S(s,0),使得直線SP與SQ斜率之積為定值,若存在求出S坐標;若不存在,請說明理由.
交于P、Q兩點,是否存在定點S(s,0),使得直線SP與SQ斜率之積為定值,若存在求出S坐標;若不存在,請說明理由.
【答案】(Ⅰ)S=2(a![]() ),S=2(a
),S=2(a![]() ),S=4a;(Ⅱ)證明見解析 (Ⅲ)存在,定點S(±3,0)
),S=4a;(Ⅱ)證明見解析 (Ⅲ)存在,定點S(±3,0)
【解析】
(Ⅰ)根據題意分桌球第一次與球桌的邊緣的接觸點為長軸的兩個端點或這兩個端點外的任一點三種情況進行討論即可.
(Ⅱ)設M(4,t),A(x1,y1),B(x2,y2),再根據橢圓在點P(x0,y0)處的切線的方程為![]() 即可求得兩條切線方程的表達式,再根據M(4,t)在兩條切線上即可求得lAB
即可求得兩條切線方程的表達式,再根據M(4,t)在兩條切線上即可求得lAB
的直線方程.
(Ⅲ)設l的方程為:x=my+1,再聯立直線與橢圓的方程,求得直線SP與SQ斜率之積的表達式,再根據表達式求S(s,0)即可.
(Ⅰ)記c![]() ,因為桌球第一次與球桌的邊緣的接觸點可能是長軸的兩個端點及這兩個端點外的任一點三種情況,
,因為桌球第一次與球桌的邊緣的接觸點可能是長軸的兩個端點及這兩個端點外的任一點三種情況,
所以,S=2(a﹣c)或S=2(a+c)或S=4a;
即S=2(a![]() ),S=2(a
),S=2(a![]() ),S=4a;
),S=4a;
(Ⅱ)設M(4,t),A(x1,y1),B(x2,y2),則直線lMA:![]() 1,lMB:
1,lMB:![]() 1,代入M中,得lMA:
1,代入M中,得lMA:![]() ty1=1,lMB:
ty1=1,lMB:![]() 2=1,
2=1,
則點A,B的坐標滿足方程:![]() ty﹣1=0,
ty﹣1=0,
恒過定點G(![]() ,0);
,0);
(Ⅲ)由已知直線過點T(1,0),設l的方程為:x=my+1,P(x,y),Q(x',y'),聯立與橢圓的方程整理得:(9+m2)y2+2my﹣8=0,∴y+y'![]() ,yy'
,yy'![]() ,
,
kSP![]() ,同理得kSQ
,同理得kSQ![]() ,∴kSPkSQ
,∴kSPkSQ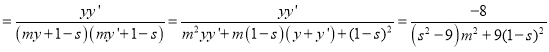 ,當s=3時,kSPkSQ
,當s=3時,kSPkSQ![]() ,
,
當s=﹣3時,kSPkSQ![]() ,所以存在定點S(±3,0),使得直線SP與SQ斜率之積為定值.
,所以存在定點S(±3,0),使得直線SP與SQ斜率之積為定值.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,焦距為6.
,焦距為6.
(1)求橢圓![]() 的方程.
的方程.
(2)過橢圓左頂點的兩條斜率之積為![]() 的直線分別與橢圓交于
的直線分別與橢圓交于![]() 點.試問直線
點.試問直線![]() 是否過某定點?若過,求出該點的坐標;若不過,請說明理由.
是否過某定點?若過,求出該點的坐標;若不過,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕頭某家電企業要將剛剛生產的100臺變頻空調送往市內某商場,現有4輛甲型貨車和8輛乙型貨車可供調配,每輛甲型貨車的運輸費用是400元,可裝空調20臺,每輛乙型貨車的運輸費用是300元,可裝空調10臺,若每輛車至多運一次,則企業所花的最少運費為( )
A. 2000元B. 2200元C. 2400元D. 2800元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率
)的離心率![]() ,直線
,直線![]() 被以橢圓
被以橢圓![]() 的短軸為直徑的圓截得的弦長為
的短軸為直徑的圓截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩個不同的點,且
兩個不同的點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一列非零向量![]() 滿足:
滿足:![]() ,
,![]() ,其中
,其中![]() 是正數
是正數
(1)求數列![]() 的通項公式;
的通項公式;
(2)求證:當![]() 時,向量
時,向量![]() 與
與![]() 的夾角為定值;
的夾角為定值;
(3)當![]() 時,把
時,把![]() 中所有與
中所有與![]() 共線的向量按原來的順序排成一列,記為
共線的向量按原來的順序排成一列,記為![]() ,令
,令![]() ,
,![]() 為坐標原點,求點列
為坐標原點,求點列![]() 的極限點
的極限點![]() 的坐標.(注:若點坐標為
的坐標.(注:若點坐標為![]() ,且
,且![]() ,則稱點
,則稱點![]() 為點列的極限點)
為點列的極限點)
查看答案和解析>>
科目:高中數學 來源: 題型:
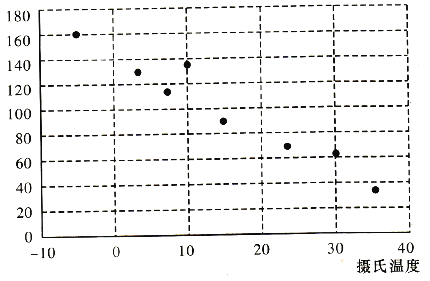
【題目】有一個同學家開了一個小賣部,他為了研究氣溫對熱飲飲料銷售的影響,經過統計,得到一個賣出的熱飲杯數與當天氣溫的散點圖和對比表:
攝氏溫度 |
|
|
|
|
|
|
|
|
熱飲杯數 |
|
|
|
|
|
|
|
|
(1)從散點圖可以發現,各點散布在從左上角到右下角的區域里。因此,氣溫與當天熱飲銷售杯數之間成負相關,即氣溫越高,當天賣出去的熱飲杯數越少。統計中常用相關系數![]() 來衡量兩個變量之間線性關系的強弱.統計學認為,對于變量
來衡量兩個變量之間線性關系的強弱.統計學認為,對于變量![]() 、
、![]() ,如果
,如果![]() ,那么負相關很強;如果
,那么負相關很強;如果![]() ,那么正相關很強;如果
,那么正相關很強;如果![]() ,那么相關性一般;如果
,那么相關性一般;如果![]() ,那么相關性較弱。請根據已知數據,判斷氣溫與當天熱飲銷售杯數相關性的強弱.
,那么相關性較弱。請根據已知數據,判斷氣溫與當天熱飲銷售杯數相關性的強弱.
(2)(i)請根據已知數據求出氣溫與當天熱飲銷售杯數的線性回歸方程;
(ii)記![]() 為不超過
為不超過![]() 的最大整數,如
的最大整數,如![]() ,
,![]() .對于(i)中求出的線性回歸方程
.對于(i)中求出的線性回歸方程![]() ,將
,將![]() 視為氣溫與當天熱飲銷售杯數的函數關系.已知氣溫
視為氣溫與當天熱飲銷售杯數的函數關系.已知氣溫![]() 與當天熱飲每杯的銷售利潤
與當天熱飲每杯的銷售利潤![]() 的關系是
的關系是![]()
![]() (單位:元),請問當氣溫
(單位:元),請問當氣溫![]() 為多少時,當天的熱飲銷售利潤總額最大?
為多少時,當天的熱飲銷售利潤總額最大?
(參考公式)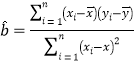 ,
,![]() ,
,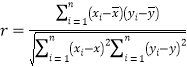
(參考數據)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:
滿足:![]() ,當
,當![]() ',
',![]() 時,
時,![]()
![]() (其中
(其中![]() 表示
表示![]() ,
,![]() ,…,
,…,![]() 中的最大項),有以下結論:
中的最大項),有以下結論:
① 若數列![]() 是常數列,則
是常數列,則![]() ;
;
② 若數列![]() 是公差
是公差![]() 的等差數列,則
的等差數列,則![]() ;
;
③ 若數列![]() 是公比為
是公比為![]() 的等比數列,則
的等比數列,則![]() :
:
④ 若存在正整數![]() ,對任意
,對任意![]() ,都有
,都有![]() ,則
,則![]() ,是數列
,是數列![]() 的最大項.
的最大項.
其中正確結論的序號是____(寫出所有正確結論的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家環境標準制定的空氣質量指數與空氣質量等級對應關系如表:
空氣質量指數 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空氣質量等級 | 1級優 | 2級良 | 3級輕 度污染 | 4級中度污染 | 5級重 度污染 | 6級嚴重污染 |
由全國重點城市環境監測網獲得10月份某五天甲城市和乙城市的空氣質量指數數據用莖葉圖表示如圖:
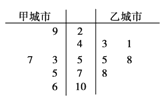
(1)試根據上面的統計數據,計算甲、乙兩個城市的空氣質量指數的方差;
(2)試根據上面的統計數據,估計甲城市某一天空氣質量等級為2級良的概率;
(3)分別從甲城市和乙城市的統計數據中任取一個,試求兩個城市空氣質量等級相同的概率.供參考數據:292+532+572+752+1062=23760,432+412+552+582+782=16003
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com