
【題目】為增強學生法治觀念,營造“學憲法、知憲法、守憲法”的良好校園氛圍,某學校開展了“憲法小衛士”活動,并組織全校學生進行法律知識競賽.現從全校學生中隨機抽取50人,統計他們的競賽成績,并得到如表所示的頻數分布表.
分數段 |
|
|
|
|
|
人數 | 5 | 15 | 15 | 12 |
|
(Ⅰ)求頻數分布表中的![]() 的值,并估計這50名學生競賽成績的中位數(精確到0.1);
的值,并估計這50名學生競賽成績的中位數(精確到0.1);
(Ⅱ)將成績在![]() 內定義為“合格”,成績在
內定義為“合格”,成績在![]() 內定義為“不合格”.請將列聯表補充完整.
內定義為“不合格”.請將列聯表補充完整.
合格 | 不合格 | 合計 | |
高一新生 | 12 | ||
非高一新生 | 6 | ||
合計 |
試問:是否有95%的把握認為“法律知識的掌握合格情況”與“是否是高一新生”有關?說明你的理由;
(Ⅲ)在(Ⅱ)的前提下,在該50人中,按“合格與否”進行分層抽樣,隨機抽取5人,再從這5人中隨機抽取2人,求恰好2人都合格的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
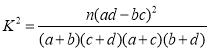 ,
,![]() .
.
【答案】(Ⅰ)![]() ,中位數73.3(Ⅱ)見解析,有(Ⅲ)0.3
,中位數73.3(Ⅱ)見解析,有(Ⅲ)0.3
【解析】
(Ⅰ)先利用樣本總數減去前面各組樣本數,即可求得![]() 的值,再利用中位數的定義列方程,即可求解;
的值,再利用中位數的定義列方程,即可求解;
(Ⅱ)根據頻數分布表,填寫2×2列聯表,再代入公式中進行計算,查表,即可得解;
(Ⅲ)先求出分層抽樣的比例,再利用枚舉法分別求得事件總數和所求的基本事件數,利用古典概型的概率公式,即可得解.
(Ⅰ)![]() .設成績的中位數為
.設成績的中位數為![]() ,
,
則![]() ,解得
,解得![]() .
.
(Ⅱ)補全2×2列聯表如下所示:
合格 | 不合格 | 合計 | |
高一新生 | 12 | 14 | 26 |
非高一新生 | 18 | 6 | 24 |
合計 | 30 | 20 | 50 |
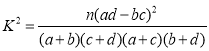
![]()
![]() ,
,
所以有95%的把握認為“法律知識的掌握合格情況”與“是否是高一新生”有關.
(Ⅲ)分層抽樣的比例為![]() ,故抽取的5人中成績合格的有
,故抽取的5人中成績合格的有![]() (人),
(人),
分別記為![]() ,
,![]() ,
,![]() ;成績不合格的有
;成績不合格的有![]() (人),分別記為
(人),分別記為![]() ,
,![]() .
.
從5人中隨機抽取2人的基本事件有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10種,
,共10種,
2人都合格的基本事件有![]() ,
,![]() ,
,![]() ,共3種,
,共3種,
所以恰好2人都合格的概率![]() .
.


科目:高中數學 來源: 題型:
【題目】已知定點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)已知定點![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點 ,則直線
兩點 ,則直線![]() 與
與![]() 斜率之積是否為定值,若是求出定值;若不是請說明理由.
斜率之積是否為定值,若是求出定值;若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
平面直角坐標系xOy中,曲線C:![]() .直線l經過點P(m,0),且傾斜角為
.直線l經過點P(m,0),且傾斜角為![]() .O為極點,以x軸正半軸為極軸,建立極坐標系.
.O為極點,以x軸正半軸為極軸,建立極坐標系.
(Ⅰ)寫出曲線C的極坐標方程與直線l的參數方程;
(Ⅱ)若直線l與曲線C相交于A,B兩點,且|PA|·|PB|=1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市正在進行創建全國文明城市的復驗工作,為了解市民對“創建全國文明城市”的知識知曉程度,某權威調查機構對市民進行隨機調查,并對調查結果進行統計,共分為優秀和一般兩類,先從結果中隨機抽取100份,統計得出如下![]() 列聯表:
列聯表:
優秀 | 一般 | 總計 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
總計 | 55 | 45 | 100 |
(1)根據上述列聯表,是否有![]() 的把握認為“創城知識的知曉程度是否為優秀與性別有關”?
的把握認為“創城知識的知曉程度是否為優秀與性別有關”?
(2)現從調查結果為一般的市民中,按分層抽樣的方法從中抽取9人,然后再從這9人中隨機抽取3人,求這三位市民中男女都有的概率;
(3)以樣本估計總體,視樣本頻率為概率,從全市市民中隨機抽取10人,用![]() 表示這10人中優秀的人數,求隨機變量
表示這10人中優秀的人數,求隨機變量![]() 的期望和方差.
的期望和方差.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
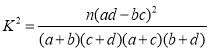 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設矩陣M=![]() (其中a>0,b>0).
(其中a>0,b>0).
(1)若a=2,b=3,求矩陣M的逆矩陣M-1;
(2)若曲線C:x2+y2=1在矩陣M所對應的線性變換作用下得到曲線C′:![]() +y2=1,求a,b的值.
+y2=1,求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
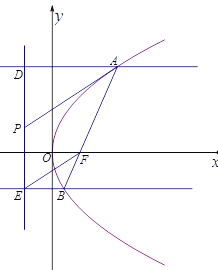
【題目】在平面直角坐標系![]() 中,已知拋物線C:
中,已知拋物線C:![]() (
(![]() )的焦點F在直線
)的焦點F在直線![]() 上,平行于x軸的兩條直線
上,平行于x軸的兩條直線![]() ,
,![]() 分別交拋物線C于A,B兩點,交該拋物線的準線于D,E兩點.
分別交拋物線C于A,B兩點,交該拋物線的準線于D,E兩點.
(1)求拋物線C的方程;
(2)若F在線段![]() 上,P是
上,P是![]() 的中點,證明:
的中點,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 、
、![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() 在線段
在線段![]() 上運動,設
上運動,設![]() .
.
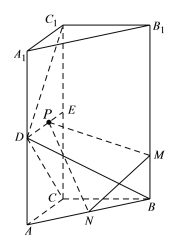
(1)證明:![]() ;
;
(2)是否存在點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成的銳二面角的大小為
所成的銳二面角的大小為![]() ?若存在,試確定點
?若存在,試確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com