
【題目】已知:函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)若函數![]() ,討論
,討論![]() 的單調性;
的單調性;
(3)若函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]() .設
.設![]() ,其中常數
,其中常數![]() 、
、![]() 滿足條件
滿足條件![]() ,且
,且![]() .試判斷在點
.試判斷在點![]() 處的切線斜率的正負,并說明理由.
處的切線斜率的正負,并說明理由.
【答案】(1)極小值1,無極大值(2) 當![]() 時,
時, ![]() 在
在![]() 上單調減;當
上單調減;當![]() 時,
時, ![]() 在
在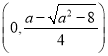 和
和 上單調減,在
上單調減,在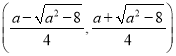 上單調增(3)在點
上單調增(3)在點![]() 處的切線斜率為正.
處的切線斜率為正.
【解析】試題分析:(1)求導,利用導函數的符號變化得到函數的單調性,進而得到函數的極值;(2)求導,討論二次項系數的符號、判別式的符號及兩根大小進行求解;(3)先將問題轉化為判斷![]() 的符號,合理構造函數進行證明.
的符號,合理構造函數進行證明.
試題解析:(1)當![]() 時,
時, ![]() ∴
∴![]() ,令
,令![]() ,則
,則![]() ,列表得:
,列表得:
|
| 1 |
|
|
| 0 |
|
| 單調減 | 極小值 | 單調增 |
∴![]() 有極小值
有極小值![]() ,無極大值;
,無極大值;
(2)![]() ,
, ![]() ∴
∴![]() ,設
,設![]()
①當![]() 時,
時, ![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴ ![]() 在
在![]() 上單調減;
上單調減;
②當![]() 且
且![]() ,即
,即![]() 時,
時, ![]() 恒成立,且不恒為0,則
恒成立,且不恒為0,則![]() 恒成立,且不恒為0,∴
恒成立,且不恒為0,∴![]() 在
在![]() 上單調減;
上單調減;
③當![]() 且
且![]() ,即
,即![]() 時,
時,
![]() 有兩個實數根:
有兩個實數根: ![]() ,且
,且![]()
∴![]() ∴當
∴當![]() 或
或![]() 時,
時, ![]() ,
, ![]() ;當
;當![]() 時,
時, ![]() ,
, ![]() ;
;
∴![]() 在
在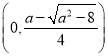 和
和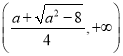 上單調減,在
上單調減,在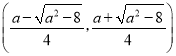 上單調增.
上單調增.
∴綜上:當![]() 時,
時, ![]() 在
在![]() 上單調減;當
上單調減;當![]() 時,
時, ![]() 在
在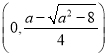 和
和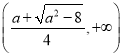 上單調減,在
上單調減,在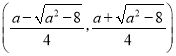 上單調增.
上單調增.
(3)![]() ,
, ![]() ,問題即為判斷
,問題即為判斷![]() 的符號.
的符號.
∵函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]()
∴![]() 兩式相減得:
兩式相減得: ![]()
∴![]()
∴![]()
![]() )
)
![]()
∵![]() 且
且![]() ∴
∴![]() ∵
∵![]() ∴
∴![]()
研究: ![]() 的符號,即判斷
的符號,即判斷![]() 的符號.
的符號.
令![]() ,
, ![]() ,設
,設![]()
∴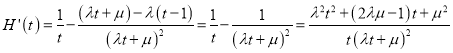
方法(一)設![]() ,其對稱軸為:
,其對稱軸為: ![]()
∴![]() 在
在![]() 上單調減,則
上單調減,則![]() ,即
,即![]() 在
在![]() 上恒成立 ∴
上恒成立 ∴![]() 在
在![]() 上單調增 ∴
上單調增 ∴![]() ,即
,即![]()
∵![]() ∴
∴![]()
∴![]() ,即
,即![]()
∴在點![]() 處的切線斜率為正.
處的切線斜率為正.
方法(二)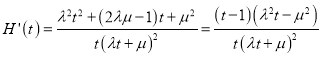
∵![]() ,
, ![]() ∴
∴![]() ∴
∴![]() 在
在![]() 上恒成立
上恒成立
∴![]() 在
在![]() 上單調增 ∴
上單調增 ∴![]() ,即
,即![]()
∵![]() ∴
∴![]()
∴![]() ,即
,即![]()
∴在點![]() 處的切線斜率為正.
處的切線斜率為正.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且cos2 ![]() =
= ![]() ,△ABC的面積為4.
,△ABC的面積為4.
(1)求 ![]() 的值;
的值;
(2)若2sinB=5sinC,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年1月,北京經歷了59年來霧霾天氣最多的一個月.據氣象局統計,北京市2013年1月1日至1月30日這30天里有26天出現霧霾天氣,《環境空氣質量指數(AQI)技術規定(試行)》如表1:
表1 空氣質量指數AQI分組表
AQI指數M | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
級別 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
狀況 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
表2是某氣象觀測點記錄的連續4天里AQI指數M與當天的空氣水平可見度y(km)的情況,表3是某氣象觀測點記錄的北京市2013年1月1日至1月30日的AQI指數頻數分布表.
表2 AQI指數M與當天的空氣水平可見度y(km)的情況
AQI指數M | 900 | 700 | 300 | 100 |
空氣水平可見度y(km) | 0.5 | 3.5 | 6.5 | 9.5 |
表3 北京市2013年1月1日至1月30日AQI指數頻數分布表
AQI指數M | [0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設x=![]() ,根據表2的數據,求出y關于x的線性回歸方程.
,根據表2的數據,求出y關于x的線性回歸方程.
(2)小王在北京開了一家洗車店,經小王統計:當AQI指數低于200時,洗車店平均每天虧損約2000元;當AQI指數在200至400時,洗車店平均每天收入約4000元;當AQI指數不低于400時,洗車店平均每天收入約7000元.
①估計小王的洗車店在2013年1月份平均每天的收入;
②從AQI指數在[0,200)和[800,1000]內的這6天中抽取2天,求這2天的收入之和不低于5000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列4個命題,其中正確命題的個數是( )
①計算:9192除以100的余數是1;
②命題“x>0,x﹣lnx>0”的否定是“x>0,x﹣lnx≤0”;
③y=tanax(a>0)在其定義域內是單調函數而且又是奇函數;
④命題p:“|a|+|b|≤1”是命題q:“對任意的x∈R,不等式asinx+bcosx≤1恒成立”的充分不必要條件.
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點在原點
的頂點在原點![]() ,對稱軸是
,對稱軸是![]() 軸,且過點
軸,且過點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)已知斜率為![]() 的直線
的直線![]() 交
交![]() 軸于點
軸于點![]() ,且與曲線
,且與曲線![]() 相切于點
相切于點![]() ,點
,點![]() 在曲線
在曲線![]() 上,且直線
上,且直線![]() 軸,
軸, ![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,判斷點
,判斷點![]() 是否共線,并說明理由.
是否共線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的右焦點為
的右焦點為![]() ,
, ![]() 是雙曲線C上的點,
是雙曲線C上的點, ![]() ,連接
,連接![]() 并延長
并延長![]() 交雙曲線C與點P,連接
交雙曲線C與點P,連接![]() ,若
,若![]() 是以
是以![]() 為頂點的等腰直角三角形,則雙曲線C的漸近線方程為( )
為頂點的等腰直角三角形,則雙曲線C的漸近線方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() ,滿足
,滿足![]() ,
,![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若關于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 的兩個零點分別在區間
的兩個零點分別在區間![]() 和
和![]() 內,求實數
內,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com