
【題目】已知函數f(x)=2cos2(x﹣ ![]() )﹣
)﹣ ![]() sin2x+1
sin2x+1
(Ⅰ)求f(x)的單調遞增區間;
(Ⅱ)當x∈( ![]() ,
, ![]() )時,若f(x)≥log2t恒成立,求 t的取值范圍.
)時,若f(x)≥log2t恒成立,求 t的取值范圍.
【答案】解:(Ⅰ)∵f(x)=cos(2x﹣ ![]() )﹣
)﹣ ![]() sin2x+2=
sin2x+2= ![]() cos2x﹣
cos2x﹣ ![]() sin2x+2=cos(2x+
sin2x+2=cos(2x+ ![]() )+2, 由2kπ﹣π≤2x+
)+2, 由2kπ﹣π≤2x+ ![]() ≤2kπ,k∈Z,得k
≤2kπ,k∈Z,得k ![]() ≤x≤k
≤x≤k ![]() ,k∈Z,
,k∈Z,
∴f(x)的單調遞增區間為[k ![]() ,k
,k ![]() ],k∈Z,.
],k∈Z,.
(或者:f(x)= ![]() ﹣
﹣ ![]() +2=
+2= ![]() cos2x﹣
cos2x﹣ ![]() +2
+2
=﹣ ![]() +2,
+2,
令 ![]() +2kπ≤
+2kπ≤ ![]() ≤
≤ ![]() +2kπ,k∈Z.
+2kπ,k∈Z.
則 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z.…(5分)
+kπ,k∈Z.…(5分)
∴f(x)的單調遞增區間為:[ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z.
+kπ],k∈Z.
(Ⅱ)∵ ![]() ,
,
∴ ![]() ,
,
∴﹣1≤cos( ![]() )≤﹣
)≤﹣ ![]() ,1≤cos(2x+
,1≤cos(2x+ ![]() )+2
)+2 ![]() ,
,
(或者:∵ ![]() ,∴
,∴ ![]()
∴ ![]() ≤
≤ ![]() ≤1∴1≤﹣
≤1∴1≤﹣ ![]() +2≤
+2≤ ![]()
∴f(x) ![]() ,f(x)min=1.
,f(x)min=1.
若f(x)≥log2t恒成立,∴則log2t≤1,
∴0<t≤2,
即t的取值范圍為(0,2]
【解析】(Ⅰ)由三角函數中的恒等變換應用化簡函數解析式可得f(x)=cos(2x+ ![]() )+2,由2kπ﹣π≤2x+
)+2,由2kπ﹣π≤2x+ ![]() ≤2kπ,k∈Z,即可解得f(x)的單調遞增區間.(Ⅱ)由
≤2kπ,k∈Z,即可解得f(x)的單調遞增區間.(Ⅱ)由 ![]() ,可得
,可得 ![]() ,解得1≤cos(2x+
,解得1≤cos(2x+ ![]() )+2
)+2 ![]() ,求得f(x)
,求得f(x) ![]() ,f(x)min=1,由題意log2t≤1,從而解得t的取值范圍.
,f(x)min=1,由題意log2t≤1,從而解得t的取值范圍.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,如果存在正實數
,如果存在正實數![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 的型增函數”,已知
的型增函數”,已知![]() 是定義在
是定義在![]() 上的奇函數,且在
上的奇函數,且在![]() 時,
時, ![]() ,若
,若![]() 為
為![]() 上的“2017的型增函數”,則實數
上的“2017的型增函數”,則實數![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,畫出該梯形的直觀圖A′B′C′D′,并寫出其做法(要求保留作圖過程的痕跡.)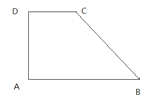
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設小明訂了一份報紙,送報人可能在早上6:30—7:30之間把報紙送到,小明離家的時間在早上7:00—8:00之間,則他在離開家之前能拿到報紙的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究小組在電腦上進行人工降雨模擬實驗,準備用A、B、C三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其實驗統計結果如下
方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 模擬實驗次數 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定對甲、乙、丙三地實施的人工降雨彼此互不影響,且不考慮洪澇災害,請根據統計數據:
(1)求甲、乙、丙三地都恰為中雨的概率;
(2)考慮不同地區的干旱程度,當雨量達到理想狀態時,能緩解旱情,若甲、丙地需中雨或大雨即達到理想狀態,乙地必須是大雨才達到理想狀態,記“甲、乙、丙三地中緩解旱情的個數”為隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側棱AA1⊥平面ABC,△ABC為等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分別是CC1 , BC的中點.
(Ⅰ)求證:B1F⊥平面AEF;
(Ⅱ)求三棱錐E﹣AB1F的體積.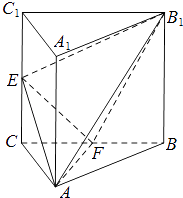
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分別求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點A(﹣1,2)為圓心的圓與直線m:x+2y+7=0相切,過點B(﹣2,0)的動直線l與圓A相交于M、N兩點
(1)求圓A的方程.
(2)當|MN|=2 ![]() 時,求直線l方程.
時,求直線l方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com