
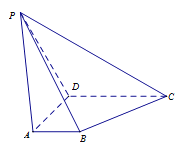
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() , 底面
, 底面![]() 為梯形,
為梯形, ![]() ,
,![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() 是棱
是棱![]() 的中點,求證:對于棱
的中點,求證:對于棱![]() 上任意一點
上任意一點![]() ,
,![]() 與
與![]() 都不平行
都不平行
【答案】(Ⅰ)見證明;(Ⅱ)見證明;(Ⅲ)見證明
【解析】
(Ⅰ)利用線面平行判定定理即可證明AB∥平面PCD.
(Ⅱ)法一:利用面面垂直的性質(zhì)即可證明AD⊥平面PCD.法二:在平面PCD中過點D作DH⊥CD,交PC于H,利用面面垂直的性質(zhì)可證DH⊥平面ABCD,進而利用線面垂直的性質(zhì)可證DH⊥AD,再根據(jù)線面垂直的判定定理即可證明AD⊥平面PCD.
(Ⅲ)法一:假設存在棱BC上點F,使得MF∥PC,連接AC,取其中點N,有MN∥PC,即可證明MF與MN重合,即MF就是MC,由MC與PC相交,矛盾,即可問題得證.法二:假設存在棱BC上點F,使得MF∥PC,顯然F與點C不同,可得P,M,F,C四點在同一個平面α中,即B∈FCα,A∈PMα,α就是點A,B,C確定的平面ABCD,且P∈α,這與P﹣ABCD為四棱錐矛盾,即可得解假設錯誤,問題得證.
(Ⅰ)因為![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
(Ⅱ)法一:
因為平面![]() 平面
平面![]()
平面![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
法二:
在平面![]() 中過點
中過點![]() 作
作![]() ,交
,交![]() 于
于![]()
因為平面![]() 平面
平面![]()
平面![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
因為![]() 平面
平面![]()
所以![]()
又![]() ,
,![]()
所以![]() 平面
平面![]()
(Ⅲ)法一:
假設存在棱![]() 上點
上點![]() ,使得
,使得![]()
連接![]() ,取其中點
,取其中點![]()
在![]() 中,因為
中,因為![]() 分別為
分別為![]() 的中點,所以
的中點,所以![]()
因為過直線外一點只有一條直線和已知直線平行,所以![]() 與
與![]() 重合
重合
所以點![]() 在線段
在線段![]() 上,所以
上,所以![]() 是
是![]() ,
,![]() 的交點
的交點![]()
即![]() 就是
就是![]()
而![]() 與
與![]() 相交,矛盾,所以假設錯誤,問題得證
相交,矛盾,所以假設錯誤,問題得證
法二:
假設存在棱![]() 上點
上點![]() ,使得
,使得![]() ,顯然
,顯然![]() 與點
與點![]() 不同
不同
所以![]() 四點在同一個平面
四點在同一個平面![]() 中
中
所以![]()
![]() ,
,![]()
![]()
所以![]()
![]() ,
,![]()
![]()
所以![]() 就是點
就是點![]() 確定的平面
確定的平面![]() ,且
,且![]()
![]()
這與![]() 為四棱錐矛盾,所以假設錯誤,問題得證
為四棱錐矛盾,所以假設錯誤,問題得證


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業(yè)系列答案
名牌中學課時作業(yè)系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數(shù)學 來源: 題型:
【題目】2020年1月10日,引發(fā)新冠肺炎疫情的COVID-9病毒基因序列公布后,科學家們便開始了病毒疫苗的研究過程.但是類似這種病毒疫苗的研制需要科學的流程,不是一朝一夕能完成的,其中有一步就是做動物試驗.已知一個科研團隊用小白鼠做接種試驗,檢測接種疫苗后是否出現(xiàn)抗體.試驗設計是:每天接種一次,3天為一個接種周期.已知小白鼠接種后當天出現(xiàn)抗體的概率為![]() ,假設每次接種后當天是否出現(xiàn)抗體與上次接種無關.
,假設每次接種后當天是否出現(xiàn)抗體與上次接種無關.
(1)求一個接種周期內(nèi)出現(xiàn)抗體次數(shù)![]() 的分布列;
的分布列;
(2)已知每天接種一次花費100元,現(xiàn)有以下兩種試驗方案:
①若在一個接種周期內(nèi)連續(xù)2次出現(xiàn)抗體即終止本周期試驗,進行下一接種周期,試驗持續(xù)三個接種周期,設此種試驗方式的花費為![]() 元;
元;
②若在一個接種周期內(nèi)出現(xiàn)2次或3次抗體,該周期結(jié)束后終止試驗,已知試驗至多持續(xù)三個接種周期,設此種試驗方式的花費為![]() 元.
元.
比較隨機變量![]() 和
和![]() 的數(shù)學期望的大小.
的數(shù)學期望的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題10分)選修4—4:坐標系與參數(shù)方程
已知曲線C1的參數(shù)方程為![]() (t為參數(shù)),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ。
(t為參數(shù)),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ。
(Ⅰ)把C1的參數(shù)方程化為極坐標方程;
(Ⅱ)求C1與C2交點的極坐標(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《最強大腦》是江蘇衛(wèi)視引進德國節(jié)目《SuperBrain》而推出的大型科學競技真人秀節(jié)目.節(jié)目籌備組透露挑選選手的方式:不但要對空間感知、照相式記憶進行考核,而且要讓選手經(jīng)過名校最權(quán)威的腦力測試,120分以上才有機會入圍.某重點高校準備調(diào)查腦力測試成績是否與性別有關,在該高校隨機抽取男、女學生各100名,然后對這200名學生進行腦力測試.規(guī)定:分數(shù)不小于120分為“入圍學生”,分數(shù)小于120分為“未入圍學生”.已知男生入圍24人,女生未入圍80人.
(1)根據(jù)題意,填寫下面的![]() 列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有
列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有![]() 以上的把握認為腦力測試后是否為“入圍學生”與性別有關;
以上的把握認為腦力測試后是否為“入圍學生”與性別有關;
性別 | 入圍人數(shù) | 未入圍人數(shù) | 總計 |
男生 | 24 | ||
女生 | 80 | ||
總計 |
(2)用分層抽樣的方法從“入圍學生”中隨機抽取11名學生,然后再從這11名學生中抽取3名參加某期《最強大腦》,設抽到的3名學生中女生的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線l1:3x﹣y﹣1=0,l2:x+2y﹣5=0,l3:x﹣ay﹣3=0不能圍成三角形,則實數(shù)a的取值可能為( )
A.1B.![]() C.﹣2D.﹣1
C.﹣2D.﹣1
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】新冠肺炎疫情期間,為確保“停課不停學”,各校精心組織了線上教學活動.開學后,某校采用分層抽樣的方法從三個年級的學生中抽取一個容量為150的樣本進行關于線上教學實施情況的問卷調(diào)查.已知該校高一年級共有學生660人,抽取的樣本中高二年級有50人,高三年級有45人.下表是根據(jù)抽樣調(diào)查情況得到的高二學生日睡眠時間(單位:h)的頻率分布表.
分組 | 頻數(shù) | 頻率 |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
合計 | 50 | 1 |
(1)求該校學生總數(shù);
(2)求頻率分布表中實數(shù)x,y,z的值;
(3)已知日睡眠時間在區(qū)間[6,6.5)的5名高二學生中,有2名女生,3名男生,若從中任選2人進行面談,則選中的2人恰好為一男一女的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠共有男女員工500人,現(xiàn)從中抽取100位員工對他們每月完成合格產(chǎn)品的件數(shù)統(tǒng)計如下:
每月完成合格產(chǎn)品的件數(shù)(單位:百件) |
|
|
|
|
|
頻數(shù) | 10 | 45 | 35 | 6 | 4 |
男員工人數(shù) | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格產(chǎn)品的件數(shù)不少于3200件的員工被評為“生產(chǎn)能手”.由以上統(tǒng)計數(shù)據(jù)填寫下面![]() 列聯(lián)表,并判斷是否有95%的把握認為“生產(chǎn)能手”與性別有關?
列聯(lián)表,并判斷是否有95%的把握認為“生產(chǎn)能手”與性別有關?
非“生產(chǎn)能手” | “生產(chǎn)能手” | 合計 | |
男員工 | |||
女員工 | |||
合計 |
(2)為提高員工勞動的積極性,工廠實行累進計件工資制:規(guī)定每月完成合格產(chǎn)品的件數(shù)在定額2600件以內(nèi)的,計件單價為1元;超出![]() 件的部分,累進計件單價為1.2元;超出
件的部分,累進計件單價為1.2元;超出![]() 件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調(diào)查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數(shù)為,求的分布列和數(shù)學期望.
件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調(diào)查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數(shù)為,求的分布列和數(shù)學期望.
附:![]() ,
,
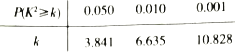 .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com