
【題目】已知f(x)=ex﹣ax2﹣2x+b(e為自然對數的底數,a,b∈R)
(1)設f′(x)為f(x)的導函數,求f′(x)的遞增區間;
(2)當a>0時,證明:f′(x)的最小值小于零;
(3)若a<0,f(x)>0恒成立,求符合條件的最小整數b.
【答案】
(1)解:令g(x)=f′(x)=ex﹣2ax﹣2,則g′(x)=ex﹣2a
當a≤0 時,g′(x)>0恒成立,此時f′(x)的單調遞增區間是(﹣∞,+∞);
當a>0,令g′(x0)=0,解得x0=ln2a,
則當x<ln2a時,g′(x)<0,g(x)單調遞減;
當x>ln2a時,g′(x)>0,g(x)單調遞增;
綜上所述,當a≤0時,f′(x)的單調遞增區間是(﹣∞,+∞);
當a>0時,f′(x)的單調遞增區間是(ln2a,+∞)
(2)證明:由(1)可知,當a>0時,x0=ln2a時,f′(x)有最小值,
則f′(x)min=g(x)min=g(ln2a)=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2
令G(x)=x﹣xlnx﹣2(x>0),G′(x)=1﹣(1+lnx)=﹣lnx,
當x∈(0,1)時,G′(x)>0,G(x)單調遞增;
當x∈(1,+∞)時,G′(x)<0,G(x)單調遞減,
∴G(x)max=G(1)=﹣1<0,∴f′(x)min<0成立
(3)解:f(x)>0恒成立,等價于f(x)min>0恒成立.
令g(x)=f′(x)=ex﹣2ax﹣2,則g′(x)=ex﹣2a,
∵a<0,∴g′(x)>0,g(x)單調遞增,
又g(0)=﹣1<0,g(1)=e﹣2a>0,
∴存在x0∈(0,1),使得g(x0)=0
則x<x0時,g(x)=f′(x)<0,f(x)單調遞減;
x>x0時,g(x)=f′(x)>0,f(x)單調遞增;
∴f(x)min=f(x0)=ex0﹣ax02﹣2x0+b>0恒成立,且ex0﹣2ax0﹣2=0
由上可知,b>﹣ex0+ax02+2x0=﹣ex0+x0( ![]() ﹣1)+2x0=(
﹣1)+2x0=( ![]() ﹣1)ex0+x0
﹣1)ex0+x0
又可得,a= ![]() <0,∴x0∈(0,ln2)
<0,∴x0∈(0,ln2)
令m(x)=( ![]() x﹣1)ex+x,x∈(0,ln2),
x﹣1)ex+x,x∈(0,ln2),
令n(x)=m′(x)= ![]() (x﹣1)ex+1,n′(x)=
(x﹣1)ex+1,n′(x)= ![]() xex>0,
xex>0,
∴n(x)>n(0)= ![]() >0,∴m(x)單調遞增,m(x)>m(0)=(﹣1)e0=﹣1,
>0,∴m(x)單調遞增,m(x)>m(0)=(﹣1)e0=﹣1,
m(x)<m(ln2)=( ![]() ﹣1)eln2+ln2=2ln2﹣2
﹣1)eln2+ln2=2ln2﹣2
∴b>﹣1,∴符合條件的最小整數b=0
【解析】(1)令g(x)=f′(x)=ex﹣2ax﹣2,求得g(x)導數,討論當a≤0 時,當a>0時,由導數大于0,可得增區間;導數小于0,可得減區間;(2)f′(x)min=g(x)min=g(ln2a)=eln2a﹣2aln2a﹣2=2a﹣2aln2a﹣2,令G(x)=x﹣xlnx﹣2(x>0),求得導數和單調區間,可得G(x)的最大值,即可得證;(3)f(x)>0恒成立,等價于f(x)min>0恒成立.令g(x)=f′(x)=ex﹣2ax﹣2,求出g(x)的零點所在區間,得到f(x)的單調區間和最小值,即f(x)min=f(x0)=ex0﹣ax02﹣2x0+b>0恒成立,且ex0﹣2ax0﹣2=0,再由參數分離和構造函數法,即可得到b的范圍,進而得到最小整數b.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減,以及對函數的最大(小)值與導數的理解,了解求函數
在這個區間單調遞減,以及對函數的最大(小)值與導數的理解,了解求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在內的極值;(2)將函數
![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】“過大年,吃水餃”是我國不少地方過春節的一大習俗,2018年春節前夕,![]() 市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標.
市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標.

(1)求所抽取的100包速凍水餃該項質量指標值的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)①由直方圖可以認為,速凍水餃的該項質量指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在
落在![]() 內的概率;
內的概率;
②將頻率視為概率,若某人從某超市購買了4包這種品牌的速凍水餃,記這4包速凍水餃中這種質量指標值位于![]() 內的包數為
內的包數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100包速凍水餃的質量指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為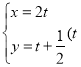 為參數),直線
為參數),直線![]() 和圓
和圓![]() 交于
交于![]() 兩點,
兩點,![]() 是圓
是圓![]() 上不同于
上不同于![]() 的任意一點.
的任意一點.
(1)求圓心的極坐標;
(2)求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學校本課程開設了A、B、C、D共4門選修課,每個學生必須且只能選修1門選修課,現有該校的甲、乙、丙3名學生:
(Ⅰ)求這3名學生選修課所有選法的總數;
(Ⅱ)求恰有2門選修課沒有被這3名學生選擇的概率;
(Ⅲ)求A選修課被這3名學生選擇的人數![]() 的分布列 .
的分布列 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線y=![]() 焦點F的直線交拋物線于A,B兩點,點C在直線y=-1上,若△ABC為正三角形,則其邊長為
焦點F的直線交拋物線于A,B兩點,點C在直線y=-1上,若△ABC為正三角形,則其邊長為
A. 11 B. 13 C. 14 D. 12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com