
【題目】如圖,已知點![]() 是
是![]() 軸下方(不含
軸下方(不含![]() 軸)一點,拋物線
軸)一點,拋物線![]() 上存在不同的兩點
上存在不同的兩點![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,其中
,其中![]() 為常數,且
為常數,且![]() 、
、![]() 兩點均在
兩點均在![]() 上,弦
上,弦![]() 的中點為
的中點為![]() .
.
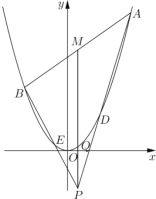
(1)若![]() 點坐標為
點坐標為![]() ,
,![]() 時,求弦
時,求弦![]() 所在的直線方程;
所在的直線方程;
(2)在(1)的條件下,如果過![]() 點的直線
點的直線![]() 與拋物線
與拋物線![]() 只有一個交點,過
只有一個交點,過![]() 點的直線
點的直線![]() 與拋物線
與拋物線![]() 也只有一個交點,求證:若
也只有一個交點,求證:若![]() 和
和![]() 的斜率都存在,則
的斜率都存在,則![]() 與
與![]() 的交點
的交點![]() 在直線
在直線![]() 上;
上;
(3)若直線![]() 交拋物線
交拋物線![]() 于點
于點![]() ,求證:線段
,求證:線段![]() 與
與![]() 的比為定值,并求出該定值.
的比為定值,并求出該定值.
【答案】(1)![]() ;(2)詳見解析;(3)證明詳見解析,定值為
;(2)詳見解析;(3)證明詳見解析,定值為![]() .
.
【解析】
(1)設![]() ,
,![]() ,得到
,得到![]() 和
和![]() ,即得
,即得![]() 的坐標,即得弦
的坐標,即得弦![]() 所在的直線方程;
所在的直線方程;
(2)先求出![]() ,
,![]() ,再求出交點
,再求出交點![]() ,即得證;
,即得證;
(3)先求出直線![]() 的方程為
的方程為![]() ,得到
,得到![]() ,
,![]() ,即得線段
,即得線段![]() 與
與![]() 的比.
的比.
(1)設![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
由![]() 點在
點在![]() 上可得:
上可得:![]() ,化簡得:
,化簡得:![]() ,同理可得:
,同理可得:
![]() ,
,
∵![]() 、
、![]() 兩點不同,不妨設
兩點不同,不妨設![]() ,
,![]() ,
,
∴弦![]() 所在的直線方程為
所在的直線方程為![]() .
.
(2)由(1)可知,![]() ,
,![]() ,設
,設![]() ,
,
與![]() 聯立,并令
聯立,并令![]() ,可得
,可得![]() ,同理
,同理![]() 的斜率
的斜率![]() ,
,
∴![]() ,
,![]() ,
,
解方程組得交點![]() ,而直線
,而直線![]() 的方程為
的方程為![]() ,得證.
,得證.
(3)設![]() ,
,![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,
代入![]() ,化簡得:
,化簡得:![]() ,
,
同理可得:![]() ,
,
顯然![]() ,∴
,∴![]() 、
、![]() 是方程
是方程![]() 的兩個不同的根,
的兩個不同的根,
∴![]() ,
,![]() ,
,
∴![]() ,即直線
,即直線![]() 的方程為
的方程為![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
所以線段![]() 與
與![]() 的比為
的比為
∴線段![]() 與
與![]() 的比為定值
的比為定值![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案科目:高中數學 來源: 題型:
【題目】某外賣平臺為提高外賣配送效率,針對外賣配送業務提出了兩種新的配送方案,為比較兩種配送方案的效率,共選取50名外賣騎手,并將他們隨機分成兩組,每組25人,第一組騎手用甲配送方案,第二組騎手用乙配送方案.根據騎手在相同時間內完成配送訂單的數量(單位:單)繪制了如下莖葉圖:
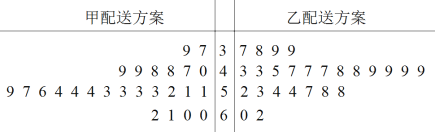
(1)根據莖葉圖,求各組內25位騎手完成訂單數的中位數,已知用甲配送方案的25位騎手完成訂單數的平均數為52,結合中位數與平均數判斷哪種配送方案的效率更高,并說明理由;
(2)設所有50名騎手在相同時間內完成訂單數的平均數![]() ,將完成訂單數超過
,將完成訂單數超過![]() 記為“優秀”,不超過
記為“優秀”,不超過![]() 記為“一般”,然后將騎手的對應人數填入下面列聯表;
記為“一般”,然后將騎手的對應人數填入下面列聯表;
優秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根據(2)中的列聯表,判斷能否有![]() 的把握認為兩種配送方案的效率有差異.
的把握認為兩種配送方案的效率有差異.
附: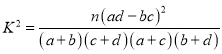 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]() 相外切,且與直線
相外切,且與直線![]() 相切.
相切.
(1)記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,求
,求![]() 的方程;
的方程;
(2)過點![]() 的兩條直線
的兩條直線![]() 與曲線
與曲線![]() 分別相交于點
分別相交于點![]() 和
和![]() ,線段
,線段![]() 和
和![]() 的中點分別為
的中點分別為![]() .如果直線
.如果直線![]() 與
與![]() 的斜率之積等于1,求證:直線
的斜率之積等于1,求證:直線![]() 經過定點.
經過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是各項均為正數的等差數列,
是各項均為正數的等差數列,![]() ,
,![]() 是
是![]() 和
和![]() 的等比中項,
的等比中項,![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通項公式;
的通項公式;
(2)設數列![]() 的通項公式
的通項公式 .
.
(i)求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(ii)求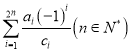 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,設
,設![]() 為線段
為線段![]() 的中點.則在
的中點.則在![]() 翻折過程中,給出如下結論:
翻折過程中,給出如下結論:
①當![]() 不在平面
不在平面![]() 內時,
內時,![]() 平面
平面![]() ;
;
②存在某個位置,使得![]() ;
;
③線段![]() 的長是定值;
的長是定值;
④當三棱錐![]() 體積最大時,其外接球的表面積為
體積最大時,其外接球的表面積為![]() .
.
其中,所有正確結論的序號是______.(請將所有正確結論的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數
的距離的比是常數![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過坐標原點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() ,
,![]() 兩點,軌跡
兩點,軌跡![]() 上異于
上異于![]() ,
,![]() 的點
的點![]() 滿足直線
滿足直線![]() 的斜率為
的斜率為![]() .
.
(ⅰ)證明:直線![]() 與
與![]() 的斜率之積為定值;
的斜率之積為定值;
(ⅱ)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,動點
為坐標原點,動點![]() 在圓
在圓![]() 上,過
上,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,點
,點![]() 滿足
滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 上的點
上的點![]() 滿足
滿足![]() .過點
.過點![]() 作直線
作直線![]() 垂直于線段
垂直于線段![]() 交
交![]() 于點
于點![]() .
.
(ⅰ)證明:![]() 恒過定點;
恒過定點;
(ⅱ)設線段![]() 交
交![]() 于點
于點![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com