
【題目】設函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞增;
上單調遞增;![]() 函數(shù)
函數(shù)![]() 在其定義域上存在極值.
在其定義域上存在極值.
(1)若![]() 為真命題,求實數(shù)
為真命題,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)如果“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,求實數(shù)
”為假命題,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)原命題等價于![]() 對
對![]() 恒成立
恒成立![]()
![]() 對
對![]() 恒成立
恒成立![]()
![]()
![]()
![]() 的取值范圍為
的取值范圍為![]() ;(2)求導得
;(2)求導得![]()
若![]() 在定義域單調遞增,在其定義域上不存在極值,不符合題意;若
在定義域單調遞增,在其定義域上不存在極值,不符合題意;若![]() ,則
,則![]() ,由
,由![]()
![]()
![]()
![]() 若
若![]() 為真命題,則
為真命題,則![]() .由已知可得
.由已知可得![]() 與
與![]() 一真一假
一真一假![]()
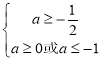 或
或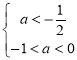
![]()
![]() .
.
綜上所述,![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析: (1)因為![]() ,
,
所以![]() 對
對![]() 恒成立,....................1分
恒成立,....................1分
因為![]() ,所以
,所以![]() 對
對![]() 恒成立,..............3分
恒成立,..............3分
所以![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]() ..............4分
..............4分
(2)對于![]() ,..............5分
,..............5分
若![]() 在定義域單調遞增,在其定義域上不存在極值,不符合題意;........6分
在定義域單調遞增,在其定義域上不存在極值,不符合題意;........6分
若![]() ,則
,則![]() ,由
,由![]() ,解得
,解得![]() ,
,
所以,若![]() 為真命題,則
為真命題,則![]() ,..............8分
,..............8分
因為“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,所以命題
”為假命題,所以命題![]() 與
與![]() 一真一假,
一真一假,
①![]() 真
真![]() 假時,
假時,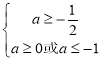 ,解得
,解得![]() ,
,
②![]() 假
假![]() 真時,
真時,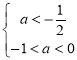 ,解得
,解得![]()
綜上所述,![]() 的取值范圍為
的取值范圍為![]() ...................12分
...................12分


科目:高中數(shù)學 來源: 題型:
【題目】已知圓M的方程為x2+(y-2)2=1,直線l的方程為x-2y=0,點P在直線l上,過點P作圓M的切線PA,PB,切點為A,B.
(Ⅰ)若∠APB=60°,試求點P的坐標;
(Ⅱ)若P點的坐標為(2,1),過P作直線與圓M交于C,D兩點,當CD=![]() 時,求直線CD的方程.
時,求直線CD的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
, ![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】類比平面內正三角形的“三邊相等,三內角相等”的性質,可推出正四面體的下列一些性質,你認為比較恰當?shù)氖牵?)
①各棱長相等,同一頂點上的任兩條棱的夾角都相等;②各個面都是全等的正三角形,相鄰兩個面所成的二面角都相等;③各個面都是全等的正三角形,同一頂點上的任兩條棱的夾角都相等。
A. ① B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在各項都不相等的等差數(shù)列{an}中,a1,a2是關于x的方程x2-7a4x+18a3=0的兩個實根.
(1) 試判斷-22是否在數(shù)列{an}中;
(2) 求數(shù)列{an}的前n項和Sn的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義區(qū)間(a,b),[a,b),(a,b],[a,b]的長度均為![]() ,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2)
,多個區(qū)間并集的長度為各區(qū)間長度之和,例如,(1,2) ![]() [3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中
[3,5)的長度d=(2-1)+(5-3)=3. 用[x]表示不超過x的最大整數(shù),記{x}=x-[x],其中![]() .設
.設![]() ,
, ![]() ,當
,當![]() 時,不等式
時,不等式![]() 解集區(qū)間的長度為
解集區(qū)間的長度為![]() ,則
,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
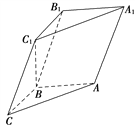
【題目】如圖,在三棱柱ABCA1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求證:C1B⊥平面ABC;
設![]() (0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
(0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
試求λ的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com