
【題目】已知集合![]() ,從P中任取2個元素,分別記為a,b.
,從P中任取2個元素,分別記為a,b.
(1)若![]() ,隨機變量X表示ab被3除的余數(shù),求
,隨機變量X表示ab被3除的余數(shù),求![]()
![]() 的概率;
的概率;
(2)若![]() (
(![]() 且
且![]() ),隨機變量Y表示
),隨機變量Y表示![]() 被5除的余數(shù),求Y的概率分布及數(shù)學(xué)期望
被5除的余數(shù),求Y的概率分布及數(shù)學(xué)期望![]() .
.
【答案】(1)![]() (2)分布列詳見解析,
(2)分布列詳見解析,![]() .
.
【解析】
(1)從10個數(shù)中任取2個數(shù)有![]() 種可能,其中
種可能,其中![]() 被3除余數(shù)為0,可分為兩類,一類兩個數(shù)是從
被3除余數(shù)為0,可分為兩類,一類兩個數(shù)是從![]() 中取得,一類是一個數(shù)從
中取得,一類是一個數(shù)從![]() 中取,一個數(shù)有其余7個數(shù)中取,這樣可得基本事件的個數(shù),從而得概率.
中取,一個數(shù)有其余7個數(shù)中取,這樣可得基本事件的個數(shù),從而得概率.
(2)把集合![]() 中的數(shù)按除以5后所得余數(shù)分成5類,
中的數(shù)按除以5后所得余數(shù)分成5類,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .隨機變量Y的可能取值為0,1,2,3,4,如事件“
.隨機變量Y的可能取值為0,1,2,3,4,如事件“![]() ”分三類:從
”分三類:從![]() 中任取2個數(shù),從
中任取2個數(shù),從![]() ,
,![]() 中各取1個數(shù),從
中各取1個數(shù),從![]() ,
,![]() 中各取1個數(shù),以上類推可求得各概率,得概率分布列,再由期望公式計算出期望.
中各取1個數(shù),以上類推可求得各概率,得概率分布列,再由期望公式計算出期望.
(1)當(dāng)![]() 時,從集合
時,從集合![]() 中任取2個元素a,b,共有
中任取2個元素a,b,共有![]() 種等可能基本事件,其中
種等可能基本事件,其中![]()
![]() 共包括
共包括![]() 種基本事件,
種基本事件,
所以![]() .
.
(2)當(dāng)![]() 時,將集合
時,將集合![]() 中元素按被5除的余數(shù)分為五類:
中元素按被5除的余數(shù)分為五類:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
因為隨機變量Y表示![]() 被5除的余數(shù),所以Y的可能取值為0,1,2,3,4.
被5除的余數(shù),所以Y的可能取值為0,1,2,3,4.
事件“![]() ”分三類:從
”分三類:從![]() 中任取2個數(shù),從
中任取2個數(shù),從![]() ,
,![]() 中各取1個數(shù),從
中各取1個數(shù),從![]() ,
,![]() 中各取1個數(shù),所以
中各取1個數(shù),所以
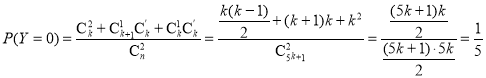
同理可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
則Y的概率分布如下:
Y | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以![]() .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優(yōu)沖刺100分系列答案
全優(yōu)沖刺100分系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分別為棱BC,PC的中點,點F在棱PA上,設(shè)
,D,E分別為棱BC,PC的中點,點F在棱PA上,設(shè)![]() .
.
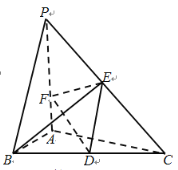
(1)當(dāng)![]() 時,求異面直線DF與BE所成角的余弦值;
時,求異面直線DF與BE所成角的余弦值;
(2)試確定t的值,使二面角C-EF-D的平面角的余弦值為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為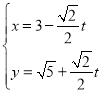 (
(![]() 為參數(shù))。在極坐標系(與直角坐標系
為參數(shù))。在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的極坐標方程為
的極坐標方程為![]() 。
。
(1)求直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)圓![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知下列兩個命題,命題甲:平面α與平面β相交;命題乙:相交直線l,m都在平面α內(nèi),并且都不在平面β內(nèi),直線l,m中至少有一條與平面β相交.則甲是乙的( )
A.充分且必要條件B.充分而不必要條件
C.必要而不充分條件D.既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了打擊海盜犯罪,甲、乙、丙三國海軍進行聯(lián)合軍事演習(xí),分別派出一艘軍艦A,B,C.演習(xí)要求:任何時刻軍艦A、B、C均不得在同一條直線上.
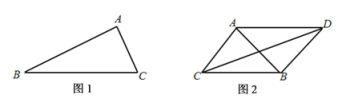
(1)如圖1,若演習(xí)過程中,A、B間的距離始終保持![]() ,B,C間的距離始終保持
,B,C間的距離始終保持![]() ,求
,求![]() 的最大值.
的最大值.
(2)如圖2,若演習(xí)過程中,A,C間的距離始終保持![]() ,B、C間的距離始終保持
,B、C間的距離始終保持![]() .且當(dāng)
.且當(dāng)![]() 變化時,模擬海盜船D始終保持:到B的距離與A、B間的距離相等,
變化時,模擬海盜船D始終保持:到B的距離與A、B間的距離相等,![]() ,與C在直線AB的兩側(cè),求C與D間的最大距離.
,與C在直線AB的兩側(cè),求C與D間的最大距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了提升學(xué)生“數(shù)學(xué)建模”的核心素養(yǎng),某校數(shù)學(xué)興趣活動小組指導(dǎo)老師給學(xué)生布置了一項探究任務(wù):如圖,有一張邊長為27cm的等邊三角形紙片ABC,從中裁出等邊三角形紙片![]() 作為底面,從剩余梯形
作為底面,從剩余梯形![]() 中裁出三個全等的矩形作為側(cè)面,圍成一個無蓋的三棱柱(不計損耗).
中裁出三個全等的矩形作為側(cè)面,圍成一個無蓋的三棱柱(不計損耗).
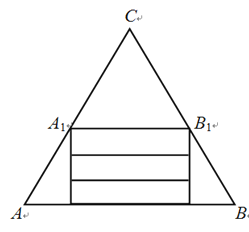
(1)若三棱柱的側(cè)面積等于底面積,求此三棱柱的底面邊長;
(2)當(dāng)三棱柱的底面邊長為何值時,三棱柱的體積最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求滿足
,求滿足![]() 的所有正整數(shù)
的所有正整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,四邊形
中,四邊形![]() 是平行四邊形,且
是平行四邊形,且![]() .
.
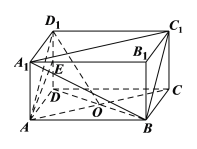
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為45°,
所成的角為45°,![]() 是
是![]() 的中點,求異面直線
的中點,求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年底,武漢發(fā)生了新冠肺炎疫情,2020年初開始蔓延.黨中央國務(wù)院面對“突發(fā)災(zāi)難”果斷采取措施,舉國上下,萬眾一心支援武漢,全國各地醫(yī)療隊陸續(xù)增援湖北,紛紛投身疫情防控與救治病人之中.為了分擔(dān)“抗疫英雄”的后顧之憂,某校教師志愿者開展“愛心輔導(dǎo)”活動,為抗疫前線醫(yī)務(wù)工作者子女開展在線輔導(dǎo).春節(jié)期間隨機安排甲乙兩位志愿者為一位初中生輔導(dǎo)功課共3次,每位志愿者至少輔導(dǎo)1次,每一次只有1位志愿者輔導(dǎo),到甲恰好輔導(dǎo)兩次的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com