
若圓C過點M(0,1)且與直線l:y=-1相切,設圓心C的軌跡為曲線E,A、B(A在y軸的右側)為曲線E上的兩點,點P(0,t)(t>0),且滿足![]() =λ
=λ![]() (λ>1).
(λ>1).
(Ⅰ)求曲線E的方程;
(Ⅱ)若t=6,直線AB的斜率為![]() ,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
(Ⅲ)分別過A、B作曲線E的切線,兩條切線交于點Q,若點Q恰好在直線l上,求證:t與![]() ·
·![]() 均為定值.
均為定值.
 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:高中數學 來源: 題型:
| AP |
| PB |
| 1 |
| 2 |
| QA |
| QB |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市海淀區高三5月查漏補缺數學試卷(解析版) 題型:解答題
若圓C過點M(0,1)且與直線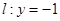 相切,設圓心C的軌跡為曲線E,A、B(A在y軸的右側)為曲線E上的兩點,點
相切,設圓心C的軌跡為曲線E,A、B(A在y軸的右側)為曲線E上的兩點,點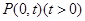 ,且滿足
,且滿足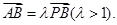
(Ⅰ)求曲線E的方程;
(Ⅱ)若t=6,直線AB的斜率為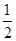 ,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
(Ⅲ)分別過A、B作曲線E的切線,兩條切線交于點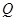 ,若點
,若點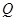 恰好在直線
恰好在直線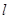 上,求證:t與
上,求證:t與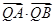 均為定值.
均為定值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省高三上學期期末考試理科數學(解析版) 題型:解答題
.(本題滿分12分)若圓C過點M(0,1)且與直線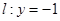 相切,設圓心C的軌跡為曲線E,A、B為曲線E上的兩點,點
相切,設圓心C的軌跡為曲線E,A、B為曲線E上的兩點,點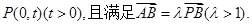
(I)求曲線E的方程; (II)若t=6,直線AB的斜率為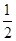 ,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
(III)分別過A、B作曲線E的切線,兩條切線交于點Q,若點Q恰好在直線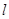 上,求證:t與
上,求證:t與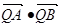 均為定值。
均為定值。
查看答案和解析>>
科目:高中數學 來源:2011年廣東省高考數學模擬試卷3(理科)(解析版) 題型:解答題
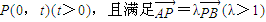 .
. ,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;
,過A、B兩點的圓N與拋物線在點A處共同的切線,求圓N的方程;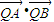 均為定值.
均為定值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com