
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() .(
.(![]() 為參數)以坐標原點
為參數)以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,點
軸的正半軸為極軸建立極坐標系,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標和 l的直角坐標方程;
的直角坐標和 l的直角坐標方程;
(2)把曲線![]() 上各點的橫坐標伸長為原來的
上各點的橫坐標伸長為原來的![]() 倍,縱坐標伸長為原來的
倍,縱坐標伸長為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,
,![]() 為
為![]() 上動點,求
上動點,求![]() 中點
中點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 底面
底面![]() ,點
,點![]() 是棱
是棱![]() 的中點.
的中點.
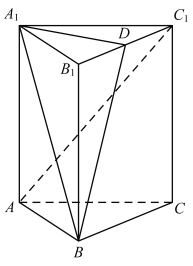
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,在棱
,在棱![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 分別是橢圓
分別是橢圓![]()
![]() 的左頂點和上頂點,
的左頂點和上頂點,![]() 為其右焦點,
為其右焦點,![]() ,且該橢圓的離心率為
,且該橢圓的離心率為![]() ;
;
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 為橢圓上的一動點,且不與橢圓頂點重合,點
為橢圓上的一動點,且不與橢圓頂點重合,點![]() 為直線
為直線![]() 與
與![]() 軸的交點,線段
軸的交點,線段![]() 的中垂線與
的中垂線與![]() 軸交于點
軸交于點![]() ,若直線
,若直線![]() 斜率為
斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且
,且![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() .(
.(![]() 為參數)以坐標原點
為參數)以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,點
軸的正半軸為極軸建立極坐標系,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標和 l的直角坐標方程;
的直角坐標和 l的直角坐標方程;
(2)把曲線![]() 上各點的橫坐標伸長為原來的
上各點的橫坐標伸長為原來的![]() 倍,縱坐標伸長為原來的
倍,縱坐標伸長為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,
,![]() 為
為![]() 上動點,求
上動點,求![]() 中點
中點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年初,由于疫情影響,開學延遲,為了不影響學生的學習,國務院、省市區教育行政部門倡導各校開展“停學不停課、停學不停教”,某校語文學科安排學生學習內容包含老師推送文本資料學習和視頻資料學習兩類,且這兩類學習互不影響已知其積分規則如下:每閱讀一篇文本資料積1分,每日上限積5分;觀看視頻1個積2分,每日上限積6分.經過抽樣統計發現,文本資料學習積分的概率分布表如表1所示,視頻資料學習積分的概率分布表如表2所示.


(1)現隨機抽取1人了解學習情況,求其每日學習積分不低于9分的概率;
(2)現隨機抽取3人了解學習情況,設積分不低于9分的人數為ξ,求ξ的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在發生某公共衛生事件期間,有專業機構認為該事件在一段時間沒有發生在規模群體感染的標志為“連續10天,每天新增疑似病例不超過7人”.根據過去10天甲、乙、丙、丁四地新增疑似病例數據,一定符合該標志的是
A. 甲地:總體均值為3,中位數為4 B. 乙地:總體均值為1,總體方差大于0
C. 丙地:中位數為2,眾數為3 D. 丁地:總體均值為2,總體方差為3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 上任意一點(異于頂點)與雙曲線兩頂點連線的斜率之積為
上任意一點(異于頂點)與雙曲線兩頂點連線的斜率之積為![]() .
.
(I)求雙曲線漸近線的方程;
(Ⅱ)過橢圓![]() 上任意一點P(P不在C的漸近線上)分別作平行于雙曲線兩條漸近線的直線,交兩漸近線于
上任意一點P(P不在C的漸近線上)分別作平行于雙曲線兩條漸近線的直線,交兩漸近線于![]() 兩點,且
兩點,且![]() ,是否存在
,是否存在![]() 使得該橢圓的離心率為
使得該橢圓的離心率為![]() ,若存在,求出橢圓方程:若不存在,說明理由.
,若存在,求出橢圓方程:若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com