
【題目】對某商店一個月內每天的顧客人數進行統計,得到樣本的莖葉圖(如圖所示).則該樣本的中位數、眾數、極差分別是( ) 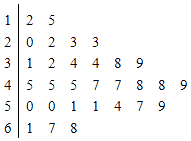
A.46 45 56
B.46 45 53
C.47 45 56
D.45 47 53
【答案】A
【解析】解:由樣本的莖葉圖得到:樣本中的30個數據從小到大排列,位于中間的兩個數據是45,47,
∴該樣本的中位數為: ![]() ;
;
出現次數最多的數據是45,∴該樣本的眾數是45;
該數據中最小值為12,最大值為68,
∴該樣本的極差為:68﹣12=56.
故選:A.
【考點精析】掌握平均數、中位數、眾數和極差、方差與標準差是解答本題的根本,需要知道⑴平均數、眾數和中位數都是描述一組數據集中趨勢的量;⑵平均數、眾數和中位數都有單位;⑶平均數反映一組數據的平均水平,與這組數據中的每個數都有關系,所以最為重要,應用最廣;⑷中位數不受個別偏大或偏小數據的影響;⑸眾數與各組數據出現的頻數有關,不受個別數據的影響,有時是我們最為關心的數據;標準差和方差越大,數據的離散程度越大;標準差和方程為0時,樣本各數據全相等,數據沒有離散性;方差與原始數據單位不同,解決實際問題時,多采用標準差.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設關于x的不等式|x﹣2|<a(a∈R)的解集為A,且 ![]() ∈A,﹣
∈A,﹣ ![]() A.
A.
(1)對任意的x∈R,|x﹣1|+|x﹣3|≥a2+a恒成立,且a∈N,求a的值.
(2)若a+b=1,a,b∈R+ , 求 ![]() +
+ ![]() 的最小值,并指出取得最小值時a的值.
的最小值,并指出取得最小值時a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市司法部門為了宣傳《憲法》舉辦法律知識問答活動,隨機對該市18~68歲的人群抽取一個容量為n的樣本,并將樣本數據分成五組:[18,28),[28,38),[38,48),[48,58),[58,68),再將其按從左到右的順序分別編號為第1組,第2組,…,第5組,繪制了樣本的頻率分布直方圖;并對回答問題情況進行統計后,結果如下表所示. 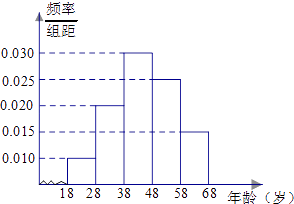
組號 | 分組 | 回答正確的人數 | 回答正確的人數占本組的比例 |
第1組 | [18,28) | 5 | 0.5 |
第2組 | [28,38) | 18 | a |
第3組 | [38,48) | 27 | 0.9 |
第4組 | [48,58) | x | 0.36 |
第5組 | [58,68) | 3 | 0.2 |
(1)分別求出a,x的值;
(2)從第2,3,4組回答正確的人中用分層抽樣方法抽取6人,則第2,3,4組每組應各抽取多少人?
(3)在(2)的前提下,決定在所抽取的6人中隨機抽取2人頒發幸運獎,求:所抽取的人中第2組至少有1人獲得幸運獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的左、右焦點,
的左、右焦點,![]() 為坐標原點,點
為坐標原點,點![]() 在橢圓上,線段
在橢圓上,線段![]() 與
與![]() 軸的交點為
軸的交點為![]() ,且
,且![]() .
.
(1)求橢圓的標準方程;
(2)圓![]() 是以
是以![]() 為直徑的圓,直線
為直徑的圓,直線![]() 與圓
與圓![]() 相切,并與橢圓交于不同的兩點
相切,并與橢圓交于不同的兩點![]() ,
,![]() ,當
,當![]() ,且滿足
,且滿足![]() 時,求
時,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
請考生在第22、23兩題中任選一題作答.注意:只能做所選定的題目.如果多做,則按所做的第一個題目計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1: 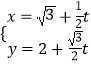 (t為參數),在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=4.
(t為參數),在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=4.
(1)求出曲線C2的直角坐標方程;
(2)若C1與C2相交于A,B兩點,求線段AB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
如圖,甲向如圖1所示的平面區域內隨機擲點、乙向如圖2所示的平面區域內隨機擲點,假設點落在區域內任意一點的可能性相同.已知圖1中小圓的半徑是大圓半徑的二分之一,圖2中小正方形的頂點為大正方形各邊的中點.
(1)甲、乙各擲點一次,求至少有一人擲點落在陰影區域的概率;
(2)甲、乙各擲點兩次,記點落在陰影區域的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.

圖1圖2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在[﹣1,1]的函數滿足f(﹣x)=﹣f(x),當a,b∈[﹣1,0)時,總有 ![]() >0(a≠b),若f(m+1)>f(2m),則實數m的取值范圍是 .
>0(a≠b),若f(m+1)>f(2m),則實數m的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,以橢圓的四個頂點為頂點的四邊形的面積為8.
,以橢圓的四個頂點為頂點的四邊形的面積為8.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)如圖,斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 的左上方.若
的左上方.若![]() ,且直線
,且直線![]() ,
, ![]() 分別與
分別與![]() 軸交于
軸交于![]() ,
, ![]() 點,求線段
點,求線段![]() 的長度.
的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com