在復平面內(nèi)， 
是原點，向量
對應的復數(shù)是
，=2+i。
（Ⅰ）如果點A關于實軸的對稱點為點B，求向量
對應的復數(shù)
和
；
（Ⅱ）復數(shù)
，
對應的點C，D。試判斷A、B、C、D四點是否在同一個圓上？并證明你的結(jié)論。
【解析】第一問中利用復數(shù)的概念可知得到由題意得，A（2,1） ∴B(2,-1)
∴ =(0,-2)
∴=-2i ∵ 
（2+i）(-2i)=2-4i,
∴ =
第二問中，由題意得，=（2,1）
∴
同理
，所以A、B、C、D四點到原點O的距離相等，
∴A、B、C、D四點在以O為圓心，
為半徑的圓上
（Ⅰ）由題意得，A（2,1） ∴B(2,-1)
∴ =(0,-2)
∴=-2i 3分
∵ （2+i）(-2i)=2-4i,
∴ = 2分
（Ⅱ）A、B、C、D四點在同一個圓上。 2分
證明：由題意得，=（2,1）
∴
同理，所以A、B、C、D四點到原點O的距離相等，
∴A、B、C、D四點在以O為圓心，為半徑的圓上
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數(shù)學 來源： 題型：
| OP |
| OA |
| OB |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
| (1+i)2 |
| 1-i |
| A、在復平面內(nèi)復數(shù)z對應的點在第一象限 | ||
B、復數(shù)z的共軛復數(shù)
| ||
| C、若復數(shù)z1=z+b（b∈R）為純虛數(shù)，則b=1 | ||
| D、設a，b為復數(shù)z的實部和虛部，則點（a，b）在以原點為圓心，半徑為1的圓上 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
對應的復數(shù)為1-i,若將
向右平移一個單位后得到
,則點A′對應的復數(shù)是( )A.1 B.1-2i
C.2-i D.-i
查看答案和解析>>
科目：高中數(shù)學 來源：山東省青島市08-09學年高二下學期期末質(zhì)檢（理） 題型：填空題
在復平面內(nèi)，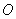
是原點，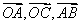
表示的復數(shù)分別為
那么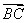
表示的復數(shù)為 ；
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
=
（Ⅱ）見解析
