
【題目】設![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)在銳角![]() 中,角
中,角![]() 的對邊分別為
的對邊分別為![]() 若
若![]() ,
, ![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)增區間![]() ,減區間為
,減區間為![]() ;(2)
;(2)![]()
【解析】試題分析:(1)將函數化為![]() ,然后根據正弦函數的單調區間求解;
,然后根據正弦函數的單調區間求解;
(2)由![]() 求得
求得![]() ,然后根據余弦定理得到
,然后根據余弦定理得到![]() ,由基本不等式可得
,由基本不等式可得![]() ,進而可得三角形面積的最大值。
,進而可得三角形面積的最大值。
試題解析:
(1)由題意知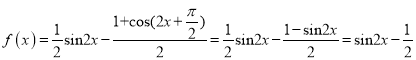 ,
,
由-![]() +2kπ≤2x≤
+2kπ≤2x≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
可得-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z;
+kπ,k∈Z;
由![]() +2kπ≤2x≤
+2kπ≤2x≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
可得![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z.
+kπ,k∈Z.
所以f(x)的單調遞增區間是[-![]() +kπ,
+kπ, ![]() +kπ](k∈Z);單調遞減區間是[
+kπ](k∈Z);單調遞減區間是[![]() +kπ,
+kπ, ![]() +kπ](k∈Z).
+kπ](k∈Z).
(2)由f(![]() )=sinA-
)=sinA-![]() =0,得sinA=
=0,得sinA=![]() ,
,
由題意知A為銳角,
所以cosA=![]() ,
,
由余弦定理得![]() ,
,
所以![]() ,當且僅當b=c時等號成立,
,當且僅當b=c時等號成立,
所以![]() ,
,
所以![]()
所以△ABC面積的最大值為![]() 。
。


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+c在x=﹣ ![]() 與x=1時都取得極值.
與x=1時都取得極值.
(1)求a、b的值與函數f(x)的單調區間;
(2)若對x∈[﹣1,2],不等式f(x)<c2恒成立,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax2+(2﹣a)x. (Ⅰ)討論f(x)的單調性;
(Ⅱ)設a>0,證明:當0<x< ![]() 時,f(
時,f( ![]() +x)>f(
+x)>f( ![]() ﹣x);
﹣x);
(Ⅲ)若函數y=f(x)的圖象與x軸交于A,B兩點,線段AB中點的橫坐標為x0 , 證明:f′(x0)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某城市有一塊半徑為40m的半圓形(以O為圓心,AB為直徑)綠化區域,現計劃對其進行改建.在AB的延長線上取點D,使OD=80m,在半圓上選定一點C,改建后的綠化區域由扇形區域AOC和三角形區域COD組成,其面積為S m2. 設∠AOC=x rad.
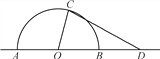
(1)寫出S關于x的函數關系式S(x),并指出x的取值范圍;
(2)張強同學說:當∠AOC=![]() 時,改建后的綠化區域面積S最大.張強同學的說法正確嗎?若不正確,請求出改建后的綠化區域面積S最大值.
時,改建后的綠化區域面積S最大.張強同學的說法正確嗎?若不正確,請求出改建后的綠化區域面積S最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin (2x+ ![]() ).
).
(1)求函數f(x)的最小正周期及其單調減區間;
(2)用“五點法”畫出函數g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的圖象(完成列表格并作圖),由圖象研究并寫出g(x)的對稱軸和對稱中心.
]的圖象(完成列表格并作圖),由圖象研究并寫出g(x)的對稱軸和對稱中心.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com