【題目】三棱柱ABC﹣A1B1C1中，△ABC為等邊三角形，AA1⊥平面ABC，AA1=AB，M，N分別是A1B1 ， A1C1的中點，則BM與AN所成角的余弦值為（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】如圖所示，由直線x=a，x=a+1（a＞0），y=x2及 x 軸圍成的曲邊梯形的面積介于相應小矩形與大矩形的面積之間，即 a2＜ 
x2dx＜（a+1）2 ． 類比之，若對n∈N*，不等式 
＜A＜ 
+ 
+…+ 
恒成立，則實數A等于（ ） 
A.ln 
B.ln 2
C.
ln 2
D. ln 5
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線 C1： 
=1（ a＞0，b＞0），圓 C2：x2+y2﹣2ax+ 
a2=0，若雙曲線C1 的一條漸近線與圓 C2 有兩個不同的交點，則雙曲線 C1 的離心率的范圍是（ ）
A.（1， 
）
B.（ ，+∞）
C.（1，2）
D.（2，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
ax2+lnx，a∈R． （Ⅰ）若曲線y=f（x）與直線y=3x+b在x=1處相切，求實數a，b的值；
（Ⅱ）求函數y=f（x）的單調區間；
（Ⅲ）若a=0時，函數h（x）=f（x）+bx有兩個不同的零點，求實數b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn ， 且a1=2，nan+1=2（n+1）an
（1）記bn= 
，求數列{bn}的通項bn；
（2）求通項an及前n項和Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C的極坐標方程ρ=2cosθ，直線l的參數方程是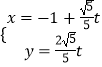 
（t為參數）． （Ⅰ）將曲線C的極坐標方程化為直角坐標方程；
（Ⅱ）設直線l與y軸的交點是M，N是曲線C上一動點，求|MN|的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，雙曲線的中心在坐標原點O，M、N分別為雙曲線虛軸的上、下端點，A是雙曲線的右頂點，F是雙曲線的右焦點，直線AM與FN相交于點P，若∠APF是銳角，則此雙曲線的離心率的取值范圍是（ ）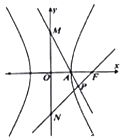 
A.（ 
，+∞）
B.（1+ 
，+∞）
C.（0， 
）
D.（ 
，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等差數列{an}前n項和為Sn ， 且S5=45，S6=60．
（1）求{an}的通項公式an；
（2）若數列{an}滿足bn+1﹣bn=an（n∈N*）且b1=3，求{ 
}的前n項和Tn ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
