
已知拋物線C:y2=4x.
(1)若橢圓左焦點及相應的準線與拋物線C的焦點F及準線l分別重合,試求橢圓短軸端點B與焦點F連線中點P的軌跡方程;
(2)若M(m,0)是x軸上的一定點,Q是(1)所求軌跡上任一點,試問|MQ|有無最小值?若有,求出其值;若沒有,說明理由.
由拋物線y2=4x,得焦點F(1,0),準線l: x=-1.
(1)設P(x,y),則B(2x-1,2y),橢圓中心O′,則|FO′|∶|BF|=e,又設點B到l的距離為d,則|BF|∶d=e,∴|FO′|∶|BF|=|BF|∶d,即(2x-2)2+(2y)2=2x(2x-2),化簡得P點軌跡方程為y2=x-1(x>1).
(2)設Q(x,y),則
|MQ|=![]()
![]()
(ⅰ)當m-![]() ≤1,即m≤
≤1,即m≤![]() 時,函數t=[x-(m-
時,函數t=[x-(m-![]() )2]+m-
)2]+m-![]() 在(1,+∞)上遞增,故t無最小值,亦即|MQ|無最小值.
在(1,+∞)上遞增,故t無最小值,亦即|MQ|無最小值.
(ⅱ)當m-![]() >1,即m>
>1,即m>![]() 時,函數t=[x2-(m-
時,函數t=[x2-(m-![]() )2]+m-
)2]+m-![]() 在x=m-
在x=m-![]() 處有最小值m-
處有最小值m-![]() ,∴|MQ|min=
,∴|MQ|min=![]() .
.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
(A)4 (B)8
(C)16 (D)32
查看答案和解析>>
科目:高中數學 來源:2013-2014學年人教版高考數學文科二輪專題復習提分訓練16練習卷(解析版) 題型:解答題
已知拋物線C:y2=2px(p>0)過點A(1,-2).
(1)求拋物線C的方程,并求其準線方程.
(2)是否存在平行于OA(O為坐標原點)的直線l,使得直線l與拋物線C有公共點,且直線OA與l的距離等于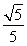 ?若存在,求出直線l的方程;若不存在,說明理由.
?若存在,求出直線l的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年人教版高考數學文科二輪專題復習提分訓練16練習卷(解析版) 題型:填空題
已知拋物線C:y2=2px(p>0)的準線為l,過M(1,0)且斜率為 的直線與l相交于點A,與C的一個交點為B,若
的直線與l相交于點A,與C的一個交點為B,若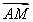 =
=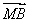 ,則p= .
,則p= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com