【題目】已知橢圓E： 
=1（a＞b＞0）過點（1， 
），左右焦點為F1、F2 ， 右頂點為A，上頂點為B，且|AB|= 
|F1F2|．
（1）求橢圓E的方程；
（2）直線l：y=﹣x+m與橢圓E交于C、D兩點，與以F1、F2為直徑的圓交于M、N兩點，且 
= 
，求m的值．
【答案】
（1）解：橢圓E： 
=1（a＞b＞0）焦點在x軸上，
∵橢圓E過點 
，
∴將點（1， 
），代入橢圓方程得 
，①
由已知 
，
∴ 
，即a2+b2=7c2②
又∵c2=a2﹣b2③，
將①②③聯立得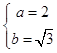 
，
∴橢圓方程為 
（2）解：根據題意，以F1、F2為直徑的圓方程為x2+y2=1，
所以圓心（0，0）到直線l的距離為 
，所以|MN|= 
，
設C（x1，y1），D（x1，y1），聯立 
，
化簡得7x2﹣8mx+4m2﹣12=0，△=48（7﹣m2）＞0，
， 
由丨CD丨= 
，
∴ 
= 
，
由 
得 
，
整理得 
，即 
，
經檢驗，當 時，△=112（7﹣m2）＞0成立，
∴
【解析】（1）由題意可知：橢圓焦點在x軸上，將點（1， ）代入橢圓方程 ，由 ，c2=a2﹣b2 ， 聯立即可求得a和b的值，即可求得橢圓E的方程；（2）圓心（0，0）到直線l的距離為 ，所以|MN|= ，將直線方程方程代入橢圓方程，由韋達定理及弦長公式可知：|CD|= ，由 得 ，整理即可求得m的值．
英才計劃同步課時高效訓練系列答案科目：高中數學 來源： 題型：
【題目】（本題滿分16分）已知函數
， 
．
（1）若函數
在
上單調遞增，求實數
的取值范圍；
（2）若直線
是函數
圖象的切線，求
的最小值；
（3）當
時，若
與
的圖象有兩個交點
，求證： 
．（取
為
，取
為
，取
為
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市政府為了實施政府績效管理、創新政府公共服務模式、提高公共服務效率．實施了“政府承諾，等你打分”民意調查活動，通過問卷調查了學生、在職人員、退休人員共250人，統計結果表不幸被污損，如表：
學生 | 在職人員 | 退休人員 | |
滿意 |
|
| 78 |
不滿意 | 5 |
| 12 |
若在所調查人員中隨機抽取1人，恰好抽到學生的概率為0.32．
（1）求滿意學生的人數；
（2）現用分層抽樣的方法在所調查的人員中抽取25人，則在職人員應抽取多少人？
（3）若滿意的在職人員為77，則從問卷調查中填寫不滿意的“學生和在職人員”中選出2人進行訪談，求這2人中包含了兩類人員的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
。
（1）若f（x）的圖象與g（x）的圖象所在兩條曲線的一個公共點在y軸上，且在該點處兩條曲線的切線互相垂直，求b和c的值。
（2）若a＝c＝1，b＝0，試比較f（x）與g（x）的大小，并說明理由；
（3）若b＝c＝0，證明：對任意給定的正數a，總存在正數m，使得當x
時，
恒有f（x）＞g（x）成立。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A、B、C對邊分別為a、b、c，sinA+sinB=2sinC，a=2b．
（1）證明：△ABC為鈍角三角形；
（2）若S△ABC= 
，求c．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
如圖，⊙O內切于△ABC的邊于D，E，F，AB=AC，連接AD交⊙O于點H，直線HF交BC的延長線于點G.
（Ⅰ）求證：圓心O在直線AD上；
（Ⅱ）求證：點C是線段GD的中點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中，正確的個數為（ ）
（1） 
（2）已知向量 
=（6，2）與 
=（﹣3，k）的夾角是鈍角，則k的取值范圍是k＜0
（3）若向量 
能作為平面內所有向量的一組基底
（4）若 
，則 在 上的投影為 
．
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn ， 點（n， 
）在直線y= 
x+ 
上． （Ⅰ）求數列{an}的通項公式；
（Ⅱ）設bn= 
，求數列{bn}的前n項和為Tn ， 并求使不等式Tn＞ 
對一切n∈N*都成立的最大正整數k的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
