
如圖,某市新體育公園的中心廣場平面圖如圖所示,在y軸左側(cè)的觀光道曲線段是函數(shù) ,
, 時的圖象且最高點B(-1,4),在y軸右側(cè)的曲線段是以CO為直徑的半圓弧.⑴試確定A,
時的圖象且最高點B(-1,4),在y軸右側(cè)的曲線段是以CO為直徑的半圓弧.⑴試確定A, 和
和 的值;⑵現(xiàn)要在右側(cè)的半圓中修建一條步行道CDO(單位:米),在點C與半圓弧上的一點D之間設(shè)計為直線段(造價為2萬元/米),從D到點O之間設(shè)計為沿半圓弧的弧形(造價為1萬元/米).設(shè)
的值;⑵現(xiàn)要在右側(cè)的半圓中修建一條步行道CDO(單位:米),在點C與半圓弧上的一點D之間設(shè)計為直線段(造價為2萬元/米),從D到點O之間設(shè)計為沿半圓弧的弧形(造價為1萬元/米).設(shè)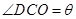 (弧度),試用
(弧度),試用 來表示修建步行道的造價預算,并求造價預算的最大值?(注:只考慮步行道的長度,不考慮步行道的寬度)
來表示修建步行道的造價預算,并求造價預算的最大值?(注:只考慮步行道的長度,不考慮步行道的寬度)
(1)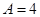 ,
,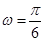 ,
,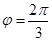 ;(2)造價預算
;(2)造價預算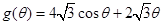 ,
,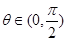 ,造價預算最大值為(
,造價預算最大值為(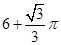 )萬元.
)萬元.
解析試題分析:(1)此小題實質(zhì)是考查利用三角函數(shù)圖像求三角解析式問題,由最高點B的坐標可求得A的值,又四分之一周期為3,易求得 ,在此情況下,把B點坐標代入三角解析式中可求得
,在此情況下,把B點坐標代入三角解析式中可求得 ;(2)本小題中步行道分兩部分組成,(如圖
;(2)本小題中步行道分兩部分組成,(如圖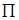 )一部分在扇形
)一部分在扇形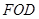 中利用弧長公式:
中利用弧長公式: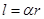 求得,另一部分在
求得,另一部分在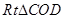 中利用直角三角形的邊角關(guān)系求得,兩項相加可得關(guān)于
中利用直角三角形的邊角關(guān)系求得,兩項相加可得關(guān)于 的造價預算函數(shù)
的造價預算函數(shù)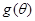 ,再用導數(shù)工具求得其最值.
,再用導數(shù)工具求得其最值.
試題解析:⑴因為最高點B(-1,4),所以A=4;又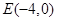 ,所以
,所以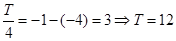 ,因為
,因為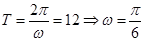 ,代入點B(-1,4),
,代入點B(-1,4),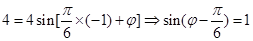 ,又
,又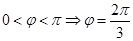 ;⑵由⑴可知:
;⑵由⑴可知: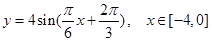 ,得點C
,得點C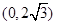 即
即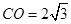 ,取CO中點F,連結(jié)DF,因為弧CD為半圓弧,所以
,取CO中點F,連結(jié)DF,因為弧CD為半圓弧,所以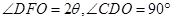 ,即
,即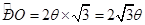 ,則圓弧段
,則圓弧段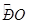 造價預算為
造價預算為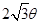 萬元,
萬元,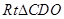 中,
中,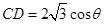 ,則直線段CD造價預算為
,則直線段CD造價預算為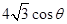 萬元,所以步行道造價預算
萬元,所以步行道造價預算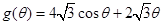 ,
,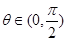 .由
.由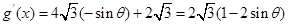 得當
得當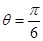 時,
時,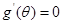 ,當
,當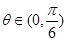 時,
時,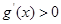 ,即
,即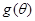 在
在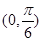 上單調(diào)遞增;當
上單調(diào)遞增;當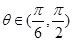 時,
時,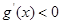 ,即
,即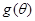 在
在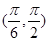 上單調(diào)遞減,所以
上單調(diào)遞減,所以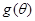 在
在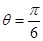 時取極大值,也即造價預算最大值為(
時取極大值,也即造價預算最大值為(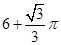 )萬元.
)萬元.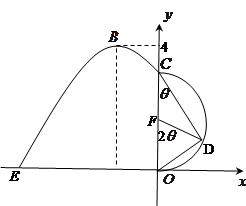 (圖
(圖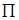 )
)
考點:利用三角函數(shù)圖像求三角解析式問題,導數(shù)求函數(shù)最值問題(要關(guān)注函數(shù)定義域),數(shù)形結(jié)合思想.


 全優(yōu)沖刺100分系列答案
全優(yōu)沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數(shù)學 來源: 題型:解答題
設(shè)函數(shù)
(1)求 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(3)畫出函數(shù) 在區(qū)間
在區(qū)間 上的圖像(完成列表并作圖)。
上的圖像(完成列表并作圖)。
(1)列表
| x | 0 | |  | |  |  |
| y | | -1 | | 1 | | |

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) ,
, .
.
(1)設(shè) 是函數(shù)
是函數(shù) 的一個零點,求
的一個零點,求 的值;
的值;
(2)求函數(shù) 的單調(diào)遞增區(qū)間.
的單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)= (sin2x-cos2x)-2sinxcosx.
(sin2x-cos2x)-2sinxcosx.
(1)求f(x)的最小正周期;
(2)設(shè)x∈[- ,
, ],求f(x)的值域和單調(diào)遞增區(qū)間.
],求f(x)的值域和單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
是否存在α∈(- ,
, ),β∈(0,π),使等式sin(3π-α)=
),β∈(0,π),使等式sin(3π-α)= cos(
cos( -β),
-β), cos(-α)=-
cos(-α)=- cos(π+β)同時成立?若存在,求出α,β的值;若不存在,請說明理由.
cos(π+β)同時成立?若存在,求出α,β的值;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com