
【題目】已知函數![]() 是
是![]() 上的奇函數.
上的奇函數.
(1)求實數![]() 的值;
的值;
(2)若![]() ,則不等式
,則不等式![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 且
且![]() 在
在![]() 上的最小值為
上的最小值為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意得出![]() ,求出
,求出![]() 的值,然后再利用奇函數的定義驗證函數
的值,然后再利用奇函數的定義驗證函數![]() 為奇函數即可;
為奇函數即可;
(2)由![]() 可得出
可得出![]() ,分析出函數
,分析出函數![]() 在
在![]() 上為增函數,再由
上為增函數,再由![]() 為奇函數,由
為奇函數,由![]() 得出關于
得出關于![]() 的不等式
的不等式![]() 在
在![]() 上有解,可得出
上有解,可得出![]() ,即可求出實數
,即可求出實數![]() 的取值范圍;
的取值范圍;
(3)由![]() 且
且![]() ,可得出
,可得出![]() ,可得出
,可得出![]() ,換元
,換元![]() ,可得出
,可得出![]() ,然后對
,然后對![]() 分
分![]() 和
和![]() ,分析二次函數
,分析二次函數![]() 在區間
在區間![]() 上的單調性,結合題中條件可求出實數
上的單調性,結合題中條件可求出實數![]() 的值.
的值.
(1)![]() 函數
函數![]() 是
是![]() 上的奇函數,
上的奇函數,![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,定義域為
,定義域為![]() ,關于原點對稱,
,關于原點對稱,
且![]() ,此時函數
,此時函數![]() 為奇函數,因此,
為奇函數,因此,![]() ;
;
(2)由(1)可知![]() ,又
,又![]() ,
,![]() ,解得
,解得![]() .
.
則函數![]() 在
在![]() 上為增函數,函數
上為增函數,函數![]() 在
在![]() 上為減函數,
上為減函數,
![]() 函數
函數![]() 在
在![]() 上是增函數且為奇函數,
上是增函數且為奇函數,
由![]() ,得
,得![]() 在
在![]() 上有解,
上有解,
![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,
上有解,
![]() ,解得
,解得![]() 或
或![]() .
.
因此,實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(3)![]() ,即
,即![]() ,
,![]() 且
且![]() ,解得
,解得![]() .
.
![]() ,令
,令![]() ,又
,又![]() ,則
,則![]() .
.
![]() ,
,![]() .
.
則![]() ,令
,令![]() ,
,
二次函數![]() 圖象的對稱軸為直線
圖象的對稱軸為直線![]() .
.
①當![]() 時,函數
時,函數![]() 在
在![]() 為增函數,
為增函數,![]() ,即
,即![]() 不合乎題意;
不合乎題意;
②當![]() 時,
時,![]() 在
在![]() 為增函數,在
為增函數,在![]() 為減函數,
為減函數,
![]() ,
,![]() 滿足.
滿足.
綜上所述,![]() .
.


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
【題目】已知函數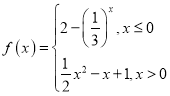 .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)畫出該函數的圖象,并寫出該函數的單調區間(不用證明);
(3)若函數![]() 恰有3個不同零點,求實數
恰有3個不同零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次體能測試中,某研究院對該地區甲、乙兩學校做抽樣調查,所得學生的測試成績如下表所示:

(1)將甲、乙兩學校學生的成績整理在所給的莖葉圖中,并分別計算其平均數;
(2)若在乙學校被抽取的10名學生中任選3人檢測肺活量,求被抽到的3人中,至少2人成績超過80分的概率;
(3)以甲學校的體能測試情況估計該地區所有學生的體能情況,則若從該地區隨機抽取4名學生,記測試成績在80分以上(含80分)的人數為![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,若雙曲線上存在點
,若雙曲線上存在點![]() ,使
,使![]() ,則該雙曲線的離心率
,則該雙曲線的離心率![]() 范圍為( )
范圍為( )
A. (1,1![]() ) B. (1,1
) B. (1,1![]() ) C. (1,1
) C. (1,1![]() ] D. (1,1
] D. (1,1![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若
,若![]() ,則稱
,則稱![]() 為
為![]() 的“不動點”;若
的“不動點”;若![]() ,則稱
,則稱![]() 為
為![]() 的“穩定點”.函數
的“穩定點”.函數![]() 的“不動點”和“穩定點”的集合分別記為
的“不動點”和“穩定點”的集合分別記為![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )設函數
)設函數![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求證:
)求證:![]() .
.
(![]() )設函數
)設函數![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下判斷正確的是 ( )
A. 函數![]() 為
為![]() 上的可導函數,則
上的可導函數,則![]() 是
是![]() 為函數
為函數![]() 極值點的充要條件
極值點的充要條件
B. 若命題![]() 為假命題,則命題
為假命題,則命題![]() 與命題
與命題![]() 均為假命題
均為假命題
C. 若![]() ,則
,則![]() 的逆命題為真命題
的逆命題為真命題
D. 在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com