【題目】5名師生站成一排照相留念，其中教師1人，男生2人，女生2人.
（1）求兩名女生相鄰而站的概率；
（2）求教師不站中間且女生不站兩端的概率.
【答案】（1）
.（2）
.
【解析】分析：（1）兩名女生站在一起有
種站法，視為一個元素與其余
個全排，有
種排法，共有不同站法
種，根據古典概型概率公式可得結果（2）教師站兩側之一，另一側由男生站，有
種站法； 兩側全由男生站，教師站除兩側和正中外的另外
個位置之一，有
種站法，共有種不同站法
，利用古典概型概率公式可得結果.
詳解：5名師生站成一排照相留念共有
種站法，
（1）記“兩名女生相鄰而站”為事件
，
兩名女生站在一起有種站法，視為一個元素與其余3個全排，有種排法，
所以事件有不同站法種，
則
，
答：兩名女生相鄰而站的概率為.
（2）記“教師不站中間且女生不站兩端”為事件
，
事件分兩類：
①教師站兩側之一，另一側由男生站，有種站法；
②兩側全由男生站，教師站除兩側和正中外的另外2個位置之一，有種站法，
所以，事件有種不同站法，
則
.
答：教師不站中間且女生不站兩端的概率為.
每課必練系列答案科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
，
，
，
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品預測如下：
甲說：“是或作品獲得一等獎”；
乙說：“作品獲得一等獎”；
丙說：“，兩項作品未獲得一等獎”；
丁說：“是作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】古希臘人常用小石子在沙灘上擺成各種形狀來研究數.比如：
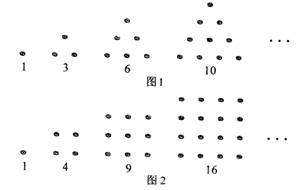
他們研究過圖1中的1，3，6，10，…，由于這些數能夠表示成三角形，將其稱為三角形數；類似的，稱圖2中的1，4，9，16，…這樣的數為正方形數.下列數中既是三角形數又是正方形數的是（ ）
A. 36 B. 45 C. 99 D. 100
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=cosxsin（x+ 
）﹣ 
cos2x+ 
，x∈R．
（1）求f（x）的最小正周期；
（2）求f（x）在閉區間[﹣ 
， ]上的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋中混裝著9個大小相同的球（編號不同），其中5只白球，4只紅球，為了把紅球與白球區分開來，采取逐只抽取檢查，若恰好經過5次抽取檢查，正好把所有白球和紅球區分出來了，則這樣的抽取方式共有__________種（用數字作答） .
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】三棱錐A﹣BCD及其側視圖、俯視圖如圖所示，設M，N分別為線段AD，AB的中點，P為線段BC上的點，且MN⊥NP．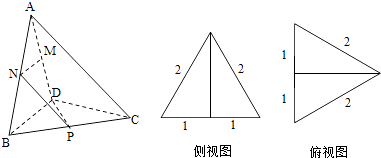 
（1）證明：P是線段BC的中點；
（2）求二面角A﹣NP﹣M的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】身體素質拓展訓練中，人從豎直墻壁的頂點A沿光滑桿自由下滑到傾斜的木板上（人可看作質點），若木板的傾斜角不同，人沿著三條不同路徑AB、AC、AD滑到木板上的時間分別為t1、t2、t3，若已知AB、AC、AD與板的夾角分別為70o、90o和105o，則（ ）
A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能確定t1、t2、t3之間的關系
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為調查乘客的候車情況，公交公司在某站臺的60名候車乘客中隨機抽取15人，將他們的候車時間（單位：分鐘）作為樣本分成5組，如下表所示：
組別 | 候車時間 | 人數 |
一 | [0，5） | 2 |
二 | [5，10） | 6 |
三 | [10，15） | 4 |
四 | [15，20） | 2 |
五 | [20，25] | 1 |
（Ⅰ）求這15名乘客的平均候車時間；
（Ⅱ）估計這60名乘客中候車時間少于10分鐘的人數；
（Ⅲ）若從上表第三、四組的6人中隨機抽取2人作進一步的問卷調查，求抽到的兩人恰好來自不同組的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
