
【題目】已知函數![]()
![]() 若
若![]() 是函數
是函數![]() 的極值點,1是函數
的極值點,1是函數![]() 的一個零點,求
的一個零點,求![]() 的值;
的值;
![]() 當
當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
![]() 若對任意
若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
【答案】(1)![]() ;(2)詳見解析;(3)
;(2)詳見解析;(3)![]() .
.
【解析】
(1)先求導得到![]() ,由
,由![]() ,
,![]() ,得到
,得到![]() 的值,繼而求出
的值,繼而求出![]() 的值;
的值;
(2)求出函數的導數,通過討論![]() 的范圍,求出函數的單調區間即可;
的范圍,求出函數的單調區間即可;
(3)令![]() ,問題轉化為
,問題轉化為![]() 上
上![]() 有解即可,亦即只需存在
有解即可,亦即只需存在![]() 使得
使得![]() 即可,連續利用導函數,然后分別對
即可,連續利用導函數,然后分別對![]() ,看是否存在
,看是否存在![]() 使得
使得![]() ,進而得到結論.
,進而得到結論.
(1)![]() ,
,
∵![]() 是函數
是函數![]() 的極值點,
的極值點,
∴![]() .
.
∵1是函數![]() 的零點,得
的零點,得![]() ,
,
由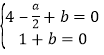 ,
,
解得![]() ,
,![]() ,
,
∴![]() ;
;
(2)![]() 時,
時,![]() ,
,![]() ,
,
![]() ,
,
![]() 時,
時,![]() ,
,![]() 遞增,
遞增,
![]() 時,令
時,令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 遞減,在
遞減,在![]() 遞增;
遞增;
(3)令![]() ,
,![]() ,則
,則![]() 為關于
為關于![]() 的一次函數且為增函數,
的一次函數且為增函數,
根據題意,對任意![]() ,都存在
,都存在![]() (
(![]() 為自然對數的底數),使得
為自然對數的底數),使得![]() 成立,
成立,
則在![]() 上
上![]() ,有解,
,有解,
令![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
由于![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,
,
①當![]() ,即
,即![]() 時,
時,![]() ,即
,即![]() ,
,![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴![]() ,不符合題意.
,不符合題意.
②當![]() ,即
,即![]() 時,
時,![]() ,
,![]()
若![]() ,則
,則![]() ,所以在
,所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴存在![]() 使得
使得![]() ,符合題意.
,符合題意.
若![]() ,則
,則![]() ,∴在
,∴在![]() 上一定存在實數
上一定存在實數![]() ,使得
,使得![]() ,
,
∴在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴存在![]() 使得
使得![]() ,符合題意.綜上所述,當
,符合題意.綜上所述,當![]() 時,對任意
時,對任意![]() ,都存在
,都存在![]() (
(![]() 為自然對數的底數),使得
為自然對數的底數),使得![]() 成立.
成立.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 與點
與點![]() 在直線
在直線![]() 的兩側,給出以下結論:①
的兩側,給出以下結論:① ![]() ;② 當
;② 當![]() 時,
時,![]() 有最小值,無最大值;③
有最小值,無最大值;③ ![]() ;④ 當
;④ 當![]() 且
且![]() 時,
時,![]() 的取值范圍是
的取值范圍是![]() ;正確的個數是( )
;正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》中給出了弦圖,所謂弦圖是由四個全等的直角三角形和中間一個小正方形拼成一個大的正方形,若圖中直角三角形兩銳角分別為![]() ,
,![]() ,且小正方形與大正方形面積之比為
,且小正方形與大正方形面積之比為![]() ,則
,則![]() 的值為( )
的值為( )
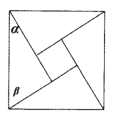
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解兒子身高與其父親身高的關系,隨機調查了5對父子的身高,統計數據如下表所示.
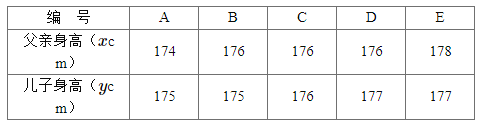
(1)從這五對父子任意選取兩對,用編號表示出所有可能取得的結果,并求隨機事件M![]() “兩對父子中兒子的身高都不低于父親的身高”發生的概率;
“兩對父子中兒子的身高都不低于父親的身高”發生的概率;
(2)由表中數據,利用“最小二乘法”求![]() 關于
關于![]() 的回歸直線的方程.
的回歸直線的方程.
參考公式: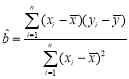 ,
,![]() ;回歸直線:
;回歸直線:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上恰有一個實數解,求
上恰有一個實數解,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若存在
,若存在![]() 使得函數
使得函數![]() 在區間
在區間![]() 上的最大值和最小值的差不超過1,求
上的最大值和最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com