
【題目】設函數![]() .
.
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 在
在![]() 處有極值,請證明:對任意
處有極值,請證明:對任意![]() 時,都有
時,都有![]() .
.
【答案】(1)當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() 和
和![]() ,單調遞減區間是
,單調遞減區間是![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() 和
和![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)見解析.
【解析】試題分析:(1)利用導數的運算法則可得![]()
![]() ,通過分類討論
,通過分類討論![]() 與2的大小關系,再根據導數與函數單調性的關系即可得出單調區間;(2)由
與2的大小關系,再根據導數與函數單調性的關系即可得出單調區間;(2)由![]() 時,
時,![]() 有極值,得到
有極值,得到![]() ,即可得到
,即可得到![]() 的值,再求出其單調遞增區間,即可得出.
的值,再求出其單調遞增區間,即可得出.
試題解析:(1)![]()
![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,解得
,解得![]() 或
或![]() ;
;![]() ,解得
,解得![]() ,
,
故函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
當![]() 時,
時,![]() ,解得
,解得![]() 或
或![]() ;
;![]() ,解得
,解得![]() ,
,
故函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
所以當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() 和
和![]() ,單調遞減區間是
,單調遞減區間是![]() ;
;
當![]() 時,
時,![]() 的單調遞增區間是
的單調遞增區間是![]() 和
和![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)∵![]() 時,
時,![]() 有極值,∴
有極值,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設命題p:f(x)=2/(x-m)在區間(1,+∞)上是減函數;;命題q:2x-1+2m>0對任意x∈R恒成立.若(![]() p)∧q為真,求實數m的取值范圍。
p)∧q為真,求實數m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市將建一個制藥廠,但該廠投產后預計每天要排放大約80噸工業廢氣,這將造成極大的環境污染.為了保護環境,市政府決定支持該廠貸款引進廢氣處理設備來減少廢氣的排放,該設備可以將廢氣轉化為某種化工產品和符合排放要求的氣體,經測算,制藥廠每天利用設備處理廢氣的綜合成本![]() (元)與廢氣處理量
(元)與廢氣處理量![]() (噸)之間的函數關系可近似地表示為
(噸)之間的函數關系可近似地表示為![]() ,且每處理
,且每處理![]() 噸工業廢氣可得價值為
噸工業廢氣可得價值為![]() 元的某種化工產品并將之利潤全部用來補貼廢氣處理.
元的某種化工產品并將之利潤全部用來補貼廢氣處理.
(1)若該制藥廠每天廢氣處理量計劃定位20噸時,那么工廠需要每天投入的廢氣處理資金為多少元?
(2)若該制藥廠每天廢氣處理量計劃定為![]() 噸,且工廠不用投入廢氣處理資金就能完成計劃的處理量,求
噸,且工廠不用投入廢氣處理資金就能完成計劃的處理量,求![]() 的取值范圍;
的取值范圍;
(3)若該制藥廠每天廢氣處理量計劃定為![]() (
(![]() )噸,且市政府決定為處理每噸廢氣至少補貼制藥廠
)噸,且市政府決定為處理每噸廢氣至少補貼制藥廠![]() 元以確保該廠完成計劃的處理量總是不用投入廢氣處理資金,求
元以確保該廠完成計劃的處理量總是不用投入廢氣處理資金,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
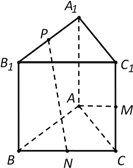
【題目】如圖,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中點,N是BC的中點,點P在線段A1B1上運動.
(Ⅰ)求證:PN⊥AM;
(Ⅱ)試確定點P的位置,使直線PN和平面ABC所成的角
最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修![]() :不等式選講
:不等式選講
已知函數f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若關于x的不等式f(x)≤|3m+1|有解,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com