
已知關于 的函數
的函數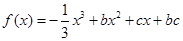 ,其導函數為
,其導函數為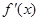 .記函數
.記函數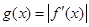 在區間
在區間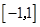 上的最大值為
上的最大值為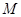 .
.
(1) 如果函數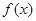 在
在 處有極值
處有極值 ,試確定
,試確定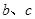 的值;
的值;
(2) 若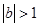 ,證明對任意的
,證明對任意的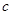 ,都有
,都有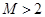 ;
;
(3) 若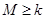 對任意的
對任意的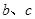 恒成立,試求
恒成立,試求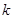 的最大值.
的最大值.
(1)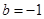 ,
,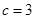 ;(2)證明詳見解析;(3)
;(2)證明詳見解析;(3)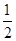 .
.
解析試題分析:本題主要考查導數的運算、利用導數求函數的極值和最值等基礎知識,考查學生的轉化能力、分析問題解決問題的能力、計算能力.第一問,先對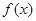 求導,由于
求導,由于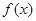 在x=1處有極值
在x=1處有極值 ,則
,則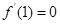 ,
,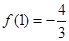 ,列出方程組,解出b和c的值,由于得到了兩組值,則需要驗證看是否符合已知條件,若不符合需舍掉;第二問,可以利用二次函數圖象和性質直接證明
,列出方程組,解出b和c的值,由于得到了兩組值,則需要驗證看是否符合已知條件,若不符合需舍掉;第二問,可以利用二次函數圖象和性質直接證明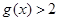 ,也可以利用反證法證明出矛盾,從而得到正確結論;第三問,結合第二問的結論,可以直接得到
,也可以利用反證法證明出矛盾,從而得到正確結論;第三問,結合第二問的結論,可以直接得到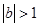 時的情況,當
時的情況,當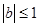 時需分
時需分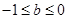 ,
,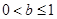 ,
,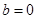 三種情況討論,最后綜合所有情況再得出結論.
三種情況討論,最后綜合所有情況再得出結論.
試題解析:(1) ∵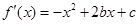 ,由
,由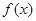 在
在 處有極值
處有極值 ,可得
,可得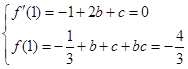 ,解得,
,解得,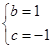 或
或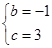 2分
2分
若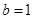 ,
,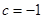 ,則
,則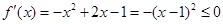 ,此時函數
,此時函數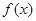 沒有極值; 3分
沒有極值; 3分
若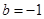 ,
,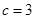 ,則
,則 ,此時當
,此時當 變化時,
變化時,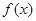 ,
,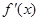 的變化情況如下表:
的變化情況如下表: