
【題目】如圖,在底面為矩形的四棱錐![]() 中,
中, ![]() .
.
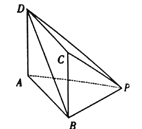
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若異面直線![]() 與
與![]() 所成角為
所成角為![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:
(1)由題意結(jié)合幾何關(guān)系可證得![]() 平面
平面![]() ,結(jié)合面面垂直的判斷定理即可證得平面
,結(jié)合面面垂直的判斷定理即可證得平面![]() 平面
平面![]() .
.
(2)建立空間直角坐標(biāo)系,結(jié)合半平面的法向量可得二面角![]() 的大小是
的大小是![]() .
.
試題解析:
(1)證明:由已知四邊形![]() 為矩形,得
為矩形,得![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:以![]() 為坐標(biāo)原點(diǎn),建立如圖所示的空間直角坐標(biāo)系
為坐標(biāo)原點(diǎn),建立如圖所示的空間直角坐標(biāo)系![]() .
.
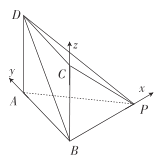
設(shè)![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,則
,則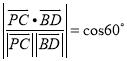 ,即
,即![]() ,
,
解得![]() (
(![]() 舍去).
舍去).
設(shè)![]() 是平面
是平面![]() 的法向量,則
的法向量,則![]() ,即
,即![]() ,
,
可取![]() .
.
設(shè)![]() 是平面
是平面![]() 的法向量,則
的法向量,則![]() 即
即![]() ,
,
可取![]() ,所以
,所以![]() ,
,
由圖可知二面角![]() 為銳角,所以二面角
為銳角,所以二面角![]() 的大小為
的大小為![]() .
.


 開心練習(xí)課課練與單元檢測(cè)系列答案
開心練習(xí)課課練與單元檢測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知y=f(x)是定義在R上的奇函數(shù),且x>0時(shí),f(x)=1+( ![]() )x
)x
(1)求函數(shù)f(x)的解析式;
(2)畫出函數(shù)f(x)的草圖; 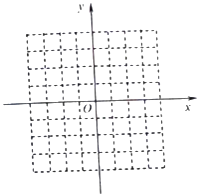
(3)利用圖象直接寫出函數(shù)f(x)的單調(diào)區(qū)間及值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓心在![]() 軸上的圓
軸上的圓![]() 過點(diǎn)
過點(diǎn)![]() 和
和![]() ,圓
,圓![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)由圓![]() 上的動(dòng)點(diǎn)
上的動(dòng)點(diǎn)![]() 向圓
向圓![]() 作兩條切線分別交
作兩條切線分別交![]() 軸于
軸于![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知:2x≤256且log2x≥ ![]() ,
,
(1)求x的取值范圍;
(2)求函數(shù)log2( ![]() )log2(
)log2( ![]() )的最大值和最小值以及相應(yīng)的x的取值.
)的最大值和最小值以及相應(yīng)的x的取值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個(gè)城市的交通狀況.在一般情況下,大橋上的車流速度v(單位:千米/小時(shí))是車流密度x(單位:輛/千米)的函數(shù).當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車流速度為0;當(dāng)車流密度不超過20輛/千米時(shí),車流速度為60千米/小時(shí).研究表明:當(dāng)![]() 時(shí),車流速度
時(shí),車流速度![]() 是車流密度
是車流密度![]() 的一次函數(shù).
的一次函數(shù).
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)當(dāng)車流密度![]() 為多大時(shí),車流量(單位時(shí)間內(nèi)通過橋上某觀測(cè)點(diǎn)的車輛數(shù),單位:輛/小時(shí))
為多大時(shí),車流量(單位時(shí)間內(nèi)通過橋上某觀測(cè)點(diǎn)的車輛數(shù),單位:輛/小時(shí))![]() 可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=x2+2ax﹣a﹣1,x∈[0,2],a為常數(shù).
(1)求f(x)的最小值g(a)的解析式;
(2)在(1)中,是否存在最小的整數(shù)m,使得g(a)﹣m≤0對(duì)于任意a∈R均成立,若存在,求出m的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種產(chǎn)品的廣告費(fèi)支出x與銷售額y(單位:萬元)之間有如表對(duì)應(yīng)數(shù)據(jù):
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求廣告費(fèi)支出x與銷售額y回歸直線方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 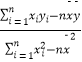 ,
, ![]()
(2)在已有的五組數(shù)據(jù)中任意抽取兩組,求至少有一組數(shù)據(jù)其預(yù)測(cè)值與實(shí)際值之差的絕對(duì)值不超過5的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 上的動(dòng)點(diǎn),過點(diǎn)
上的動(dòng)點(diǎn),過點(diǎn)![]() 作
作![]() 軸的垂線段
軸的垂線段![]() ,
, ![]() 為垂足,點(diǎn)
為垂足,點(diǎn)![]() 滿足
滿足![]() .
.
(Ⅰ)求動(dòng)點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若![]() 兩點(diǎn)分別為橢圓
兩點(diǎn)分別為橢圓![]() 的左右頂點(diǎn),
的左右頂點(diǎn), ![]() 為橢圓
為橢圓![]() 的左焦點(diǎn),直線
的左焦點(diǎn),直線![]() 與橢圓
與橢圓![]() 交于點(diǎn)
交于點(diǎn)![]() ,直線
,直線![]() 的斜率分別為
的斜率分別為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com