
【題目】f(x)是定義在(0,+∞)上的減函數,滿足f(x)+f(y)=f(xy).
(1)求證: ![]() ;
;
(2)若f(4)=﹣4,解不等式 ![]() .
.
【答案】
(1)證明:∵f(x)+f(y)=f(xy),
將x代換為 ![]() ,則有
,則有 ![]() ,
,
∴ ![]() ;
;
(2)解:∵f(x)+f(y)=f(xy),
∴﹣12=﹣4+(﹣4)+(﹣4)=f(4)+f(4)+f(4)=f(64),
∵ ![]() ,
,
∴f(x)﹣f( ![]() )=f[x(x﹣12)],
)=f[x(x﹣12)],
∴不等式 ![]() 等價于f[x(x﹣12)]≥f(64),
等價于f[x(x﹣12)]≥f(64),
∵f(x)是定義在(0,+∞)上的減函數,
∴  ,即
,即  ,
,
∴12<x≤16,
∴不等式 ![]() 的解集為{x|12<x≤16}.
的解集為{x|12<x≤16}.
【解析】
【考點精析】本題主要考查了函數單調性的性質的相關知識點,需要掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集才能正確解答此題.


科目:高中數學 來源: 題型:
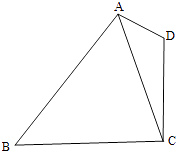
【題目】如圖,在平面四邊形ABCD中,AD=1,CD=2,AC= ![]() .
. 
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 若Sn=2an﹣3n.
(Ⅰ)求證:數列{an+3}是等比數列,并求出數列{an}的通項an;
(Ⅱ)求數列{nan}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,異面直線AD1與BD所成的角為;若AB的中點為M,DD1的中點為N,則異面直線B1M與CN所成的角為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,斜三棱柱ABC﹣A1B1C1的所有棱長均為a,M是BC的中點,側面B1C1CB⊥底面ABC,且AC1⊥BC.
(Ⅰ)求證:BC⊥C1M;
(Ⅱ)求二面角A1﹣AB﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣alnx(a∈R)
(1)當a=2時,求曲線y=f(x)在點A(1,f(1))處的切線方程;
(2)求函數f(x)的單調區間和極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓C: ![]() =1(a>b>0).設t>0,過點T(0,t)斜率為k的 直線l與橢圓C交于M,N兩點,O為坐標原點.
=1(a>b>0).設t>0,過點T(0,t)斜率為k的 直線l與橢圓C交于M,N兩點,O為坐標原點.
(Ⅰ)用a,b,k,t表示△OMN的面積S,并說明k,t應滿足的條件;
(Ⅱ)當k變化時,求S的最大值g(t).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com