【答案】
分析:本題考查的是數列與不等式的綜合類問題.在解答的過程當中:
(1)首先利用條件和通項與前n項和的關系即可轉化出數列a
n的通項之間的關系,進而即可獲得數列{a
n}的通項公式;
(2)首先利用第(1)問的結論即可將T
n化簡,再利用數學歸納法判斷T
n的單調性,由單調性即可獲得①的解答,進而由單調性即可獲得的最大值從而可以結合②中的恒成立問題進行轉化即可獲得問題的解答.
解答:解:(1)由題意可知:na
n+1=S
n+n(n+1)
∴(n-1)a
n=S
n-1+(n-1)n
兩式相減可得:a
n+1-a
n=2
所以數列{a
n}為以2為首項以2為公差的等差數列.
∴a
n=2+(n-1)•2=2n
∴數列{a
n}的通項公式:a
n=2n,n∈N*
(2)由(1)知:
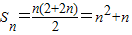
∴
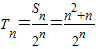
,
∴
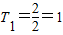
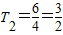
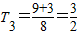
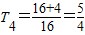
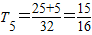
…
可猜測當n≥3時,數列{a
n}為單調遞減數列,當n≤2時,數列{a
n}為單調遞增數列.
對“當n≥3時,數列{a
n}為單調遞減數列”證明如下:
當n=3時,
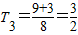
當n=4時,
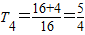
,∴T
4<T
3假設當n=k時成立,即T
k<T
k-1,∴
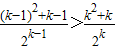
則當n=k+1時,
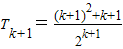
=
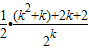
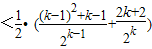
=
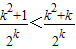
故當n=k+1時猜測成立.綜上可知:當n≥3時,數列{a
n}為單調遞減數列,當n≤2時,數列{a
n}為單調遞增數列.
又因為:對一切正整數n,總有T
n≤m,且T
n的最大值為

,所以
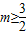
.
∴當n≥3時,T
n>T
n+1,
m的取值范圍為:
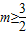
.
點評:本題考查的是數列與不等式的綜合類問題.在解答的過程當中充分體現了數列通項與數列前n項和的知識、數列與函數的思想、單調性的研究以及恒成立問題的解答規律.值得同學們體會和反思.

 ,①當n為何值時,Tn>Tn+1,②若對一切正整數n,總有Tn≤m,求m的取值范圍.
,①當n為何值時,Tn>Tn+1,②若對一切正整數n,總有Tn≤m,求m的取值范圍.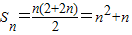
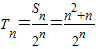 ,
,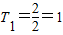
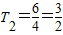
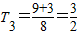
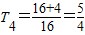
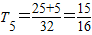
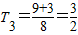
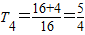 ,∴T4<T3
,∴T4<T3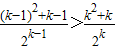
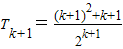 =
=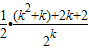
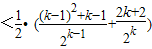
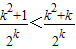
 ,所以
,所以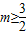 .
.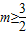 .
.
