
【題目】設![]() 、
、![]() 、
、![]() 、
、![]() 為平面直角坐標系中兩兩不同的點。若
為平面直角坐標系中兩兩不同的點。若![]() ,
,![]() ,且
,且![]() ,則稱點
,則稱點![]() 、
、![]() 調和分割點
調和分割點![]() 、
、![]() 。已知平面上點
。已知平面上點![]() 、
、![]() 調和分割點
調和分割點![]() 、
、![]() .則下面說法正確的是()。
.則下面說法正確的是()。
A. ![]() 可能是線段
可能是線段![]() 的中點
的中點
B. ![]() 可能是線段
可能是線段![]() 的中點
的中點
C. 點![]() 、
、![]() 可能同時在線段
可能同時在線段![]() 上
上
D. 點![]() 、
、![]() 不可能同時在線段
不可能同時在線段![]() 的延長線上
的延長線上
科目:高中數學 來源: 題型:
【題目】如圖,棱長為1的正方體![]() 中,點P是線段
中,點P是線段![]() 上的動點.當
上的動點.當![]() 在平面
在平面![]() ,平面
,平面![]() ,平面ABCD上的正投影都為三角形時,將它們的面積分別記為
,平面ABCD上的正投影都為三角形時,將它們的面積分別記為![]() ,
,![]() ,
,![]() .
.

(1)當![]() 時,
時,![]() ________
________![]() (用“>”或“=”或“<”填空);
(用“>”或“=”或“<”填空);
(2)![]() 的最大值為________.
的最大值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知M,N是焦點為F的拋物線y2=2px(p>0)上兩個不同的點,線段MN的中點A的橫坐標為![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直線MN與x軸交于點B,求點B的橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面ABCD,底部ABCD為菱形,E為CD的中點.
平面ABCD,底部ABCD為菱形,E為CD的中點.

(Ⅰ)求證:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求證:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在點F,使得CF∥平面PAE?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一幾何體的平面展開圖,其中四邊形![]() 為正方形,
為正方形,![]() 分別為
分別為![]() 的中點.在此幾何體中,給出下列結論,其中正確的結論是( )
的中點.在此幾何體中,給出下列結論,其中正確的結論是( )

A.平面![]() 平面
平面![]() B.直線
B.直線![]() 平面
平面![]()
C.直線![]() 平面
平面![]() D.直線
D.直線![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左焦點為
的左焦點為![]() ,過點
,過點![]() 的直線交橢圓于
的直線交橢圓于![]() ,
,![]() 兩點,
兩點,![]() 的最大值是
的最大值是![]() ,
,![]() 的最小值是
的最小值是![]() ,且滿足
,且滿足![]() .
.
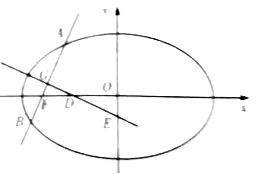
(1)求橢圓的離心率;
(2)設線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的垂直平分線與
的垂直平分線與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,
兩點,![]() 是坐標原點,記
是坐標原點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABCA1B1C1中(側棱與底面垂直的棱柱),AC=BC=1,∠ACB=90°,AA1=![]() ,D 是A1B1的中點.
,D 是A1B1的中點.

(1)求證:C1D⊥平面AA1B1B;
(2)當點F 在BB1上的什么位置時,AB1⊥平面C1DF ?并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高二年級組織外出參加學業水平考試,出行方式為:乘坐學校定制公交或自行打車前往,大數據分析顯示,當![]() 的學生選擇自行打車,自行打車的平均時間為
的學生選擇自行打車,自行打車的平均時間為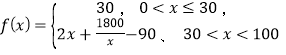 (單位:分鐘) ,而乘坐定制公交的平均時間不受
(單位:分鐘) ,而乘坐定制公交的平均時間不受![]() 影響,恒為40分鐘,試根據上述分析結果回答下列問題:
影響,恒為40分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,乘坐定制公交的平均時間少于自行打車的平均時間?
在什么范圍內時,乘坐定制公交的平均時間少于自行打車的平均時間?
(2)求該校學生參加考試平均時間![]() 的表達式:討論
的表達式:討論![]() 的單調性,并說明其實際意義.
的單調性,并說明其實際意義.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com