【題目】某校為了紀念“中國紅軍長征90周年”，增強學生對“長征精神”的深刻理解，在全校組織了一次有關“長征”的知識競賽，經過初賽、復賽，甲、乙兩個代表隊(每隊3人)進入了決賽，規定每人回答一個問題，答對為本隊贏得20分，答錯得0分.假設甲隊中每人答對的概率均為 
，乙隊中3人答對的概率分別為 
， ， 
，且各人回答正確與否相互之間沒有影響，用 
表示乙隊的總得分.
（1）求 的分布列和均值；
（2）求甲、乙兩隊總得分之和等于40分且甲隊獲勝的概率.
【答案】
（1）解：由題意知， 
的所有可能取值為0，20，40，60.
，
，
，
.
的分布列為：
| 0 | 20 | 40 | 60 |
|
|
|
|
|
所以 
.
（2）解：記“甲隊得40分，乙隊得0分”為事件 
.
又 
，
故甲、乙兩隊總得分之和為40分且甲隊獲勝的概率為： 
.
【解析】（1）明確 的所有可能取值，并確定相應的概率，從而得到分布列及期望；（2）記“甲隊得40分，乙隊得0分”為事件 ，則 。
【考點精析】關于本題考查的離散型隨機變量及其分布列，需要了解在射擊、產品檢驗等例子中，對于隨機變量X可能取的值，我們可以按一定次序一一列出，這樣的隨機變量叫做離散型隨機變量．離散型隨機變量的分布列：一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn，X取每一個值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，則稱表為離散型隨機變量X 的概率分布，簡稱分布列才能得出正確答案．
陽光課堂同步練習系列答案科目：高中數學 來源： 題型：
【題目】（1）兩個共軛復數的差是純虛數；（2）兩個共軛復數的和不一定是實數；（3）若復數a+bi（a，b∈R）是某一元二次方程的根，則a﹣bi是也一定是這個方程的根；（4）若z為虛數，則z的平方根為虛數，
其中正確的個數為（ ）
A.3
B.2
C.1
D.0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數fn（x）= 
x3﹣ 
（n+1）x2+x（n∈N*），數列{an}滿足an+1=f'n（an），a1=3．
（1）求a2 ， a3 ， a4；
（2）根據（1）猜想數列{an}的通項公式，并用數學歸納法證明；
（3）求證： 
+ 
+…+ 
＜ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓 
的離心率為 
，其中左焦點為 
.
（1）求橢圓 
的方程；
（2）過 
的直線 
與橢圓 相交于 
兩點，若 
的面積為 
，求以 
為圓心且與直線 相切的圓的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，游客從某旅游景區的景點
處下上至
處有兩種路徑．一種是從沿直線步行到，另一種是先從沿索道乘纜車到
，然后從沿直線步行到．現有甲、乙兩位游客從處下山，甲沿
勻速步行，速度為
．在甲出發
后，乙從乘纜車到，在處停留
后，再從勻速步行到，假設纜車勻速直線運動的速度為
，山路長為1260
，經測量
，
．
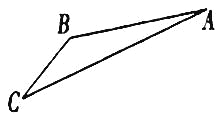
（1）求索道
的長；
（2）問：乙出發多少
后，乙在纜車上與甲的距離最短？
（3）為使兩位游客在處互相等待的時間不超過
，乙步行的速度應控制在什么范圍內？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】雙曲線 
=1（a＞1，b＞0）的焦點距為2c，直線l過點（a，0）和（0，b），且點（1，0）到直線l的距離與點（﹣1，0）到直線l的距離之和 
．求雙曲線的離心率e的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn ， 滿足an= 
+2n﹣2，n∈N* ， 且S2=6．
（1）求數列{an}的通項公式；
（2）證明： 
+ 
+ 
+…+ 
＜ 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
