已知圓
交于
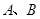兩點.
（1）求過A、B兩點的直線方程;
（2）求過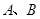兩點且圓心在直線
上的圓的方程.
（1）
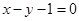；（2）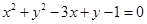
解析試題分析：（1）兩個圓的方程相減，得直線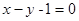
，因為圓和圓的公共點為
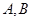，所以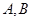點的坐標滿足方程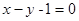，而兩點只能確定一條直線，所以過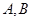兩點的直線方程為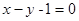，如果已知兩個圓相切，那么相減得到的是公切線方程；（2）利用過兩圓交點的直線系方程可設為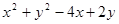
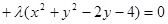
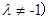，整理為圓的一般方程，進而求出圓心，再把圓心坐標
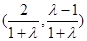代入直線中，求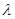
，或者該題可以先求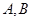兩點的坐標，在利用到圓心的距離相等列方程，求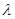試題解析：（I）聯立
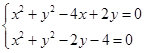，兩式相減并整理得：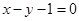
∴過A、B兩點的直線方程為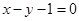 5分
（II）依題意：設所求圓的方程為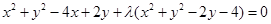
6分
其圓心坐標為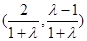 ，因為圓心在直線上，所以
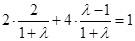，解得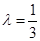
∴所求圓的方程為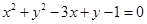： 12分
考點：1、直線的方程；2、圓的方程.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，已知直線
的斜率為
.
，求直線
軸、
軸上的截距之和為
，求直線
，
， 且它的對角線的交點是M（3，3），求這個平行四邊形其它兩邊所在直線的方程.
點射出，到
軸上的
點后，被
,求
所在直線的方程及點
，求分別滿足下列條件的直線方程：
； 
被兩平行直線
所截得的線段長為3，且直線過點（1，0），求直線
經過點
．
，求直線
和點
到直線
和直線
交點
的坐標；
經過點