
【題目】已知數列{an}的前n項和為Sn,且滿足Sn+n=2an(n∈N*).
(1)證明:數列{an+1}為等比數列,并求數列{an}的通項公式;
(2)若bn=(2n+1)an+2n+1,數列{bn}的前n項和為Tn.求滿足不等式![]() >2010的n的最小值.
>2010的n的最小值.
【答案】(1)an=2n-1,n∈N*;(2)n的最小值為10.
【解析】試題分析:本題屬于基礎題.對已知條件![]() ,用
,用![]() 代替
代替![]() 得
得![]() ,兩式相減可得
,兩式相減可得![]() ,湊配得
,湊配得![]() ,由此可證得
,由此可證得![]() 是等比數列,從而求出通項公式,這是已知數列前
是等比數列,從而求出通項公式,這是已知數列前![]() 項和與項之間關系的一般處理方法;(2)由(1)可得
項和與項之間關系的一般處理方法;(2)由(1)可得![]() ,采用錯位相減法可求出其前
,采用錯位相減法可求出其前![]() 項和
項和![]()
![]() ,不等式>2 010就轉化為
,不等式>2 010就轉化為![]() ,可知n的最小值是10.
,可知n的最小值是10.
試題解析:(1)因為Sn+n=2an,所以Sn-1=2an-1-(n-1)(n≥2,n∈N*).兩式相減,得an=2an-1+1.
所以an+1=2(an-1+1)(n≥2,n∈N*),所以數列{an+1}為等比數列.
因為Sn+n=2an,令n=1得a1=1.
a1+1=2,所以an+1=2n,所以an=2n-1.
(2)因為bn=(2n+1)an+2n+1,所以bn=(2n+1)·2n.
所以Tn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n, ①
2Tn=3×22+5×23+…+(2n-1)·2n+(2n+1)·2n+1, ②
①-②,得-Tn=3×2+2(22+23+…+2n)-(2n+1)·2n+1
=6+2×-(2n+1)·2n+1
=-2+2n+2-(2n+1)·2n+1=-2-(2n-1)·2n+1.
所以Tn=2+(2n-1)·2n+1.
若>2 010,
則>2 010,即2n+1>2 010.
由于210=1 024,211=2 048,所以n+1≥11,即n≥10.
所以滿足不等式>2 010的n的最小值是10.


科目:高中數學 來源: 題型:
【題目】已知某中學聯盟舉行了一次“盟校質量調研考試”活動,為了解本次考試學生的某學科成績情況,從中抽取部分學生的分數(滿分為![]() 分,得分取正整數,抽取學生的分數均在
分,得分取正整數,抽取學生的分數均在![]() 之內)作為樣本(樣本容量為
之內)作為樣本(樣本容量為![]() )進行統計,按照
)進行統計,按照![]() 的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在![]() 的數據)
的數據)

(Ⅰ)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(Ⅱ)在選取的樣本中,從成績在![]() 分以上(含
分以上(含![]() 分)的學生中隨機抽取
分)的學生中隨機抽取![]() 名學生參加“省級學科基礎知識競賽”,求所抽取的
名學生參加“省級學科基礎知識競賽”,求所抽取的![]() 名學生中恰有一人得分在
名學生中恰有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高爾頓(釘)板是在一塊豎起的木板上釘上一排排互相平行、水平間隔相等的圓柱形鐵釘(如圖),并且每一排釘子數目都比上一排多一個,一排中各個釘子恰好對準上面一排兩相鄰鐵釘的正中央.從入口處放入一個直徑略小于兩顆釘子間隔的小球,當小球從兩釘之間的間隙下落時,由于碰到下一排鐵釘,它將以相等的可能性向左或向右落下,接著小球再通過兩鐵釘的間隙,又碰到下一排鐵釘.如此繼續下去,在最底層的5個出口處各放置一個容器接住小球.

(Ⅰ)理論上,小球落入4號容器的概率是多少?
(Ⅱ)一數學興趣小組取3個小球進行試驗,設其中落入4號容器的小球個數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,且
,且![]() 對任意正整數
對任意正整數![]() 都成立,數列
都成立,數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在實數k,使數列![]() 是公比不為1的等比數列,且任意相鄰三項
是公比不為1的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列,若存在,求出所有k的值;若不存在,請說明理由;
按某順序排列后成等差數列,若存在,求出所有k的值;若不存在,請說明理由;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中央政府為了應對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”.為了了解人們]對“延遲退休年齡政策”的態度,責成人社部進行調研.人社部從網上年齡在15![]() 65歲的人群中隨機調查100人,調査數據的頻率分布直方圖和支持“延遲退休”的人數與年齡的統計結果如下:
65歲的人群中隨機調查100人,調査數據的頻率分布直方圖和支持“延遲退休”的人數與年齡的統計結果如下:
年齡 |
|
|
|
|
|
支持“延遲退休”的人數 | 15 | 5 | 15 | 28 | 17 |
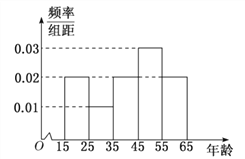
(1)由以上統計數據填![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
45歲以下 | 45歲以上 | 總計 | |
支持 | |||
不支持 | /td> | ||
總計 |
(2)若以45歲為分界點,從不支持“延遲退休”的人中按分層抽樣的方法抽取8人參加某項活動.現從這8人中隨機抽2人
①抽到1人是45歲以下時,求抽到的另一人是45歲以上的概率.
②記抽到45歲以上的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年![]() 月湖北潛江將舉辦第六屆“中國湖北(潛江)龍蝦節”,為了解不同年齡的人對“中國湖北(潛江)龍蝦節”關注程度,某機構隨機抽取了年齡在
月湖北潛江將舉辦第六屆“中國湖北(潛江)龍蝦節”,為了解不同年齡的人對“中國湖北(潛江)龍蝦節”關注程度,某機構隨機抽取了年齡在![]() 歲之間的
歲之間的![]() 人進行調查,經統計“年輕人”與“中老年人”的人數之比為
人進行調查,經統計“年輕人”與“中老年人”的人數之比為![]() .
.
關注 | 不關注 | 合計 | |
年輕人 |
| ||
中老年人 | |||
合計 |
|
|
|
(1)根據已知條件完成上面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為關注“中國湖北(潛江)龍蝦節”是否和年齡段有關?
的把握認為關注“中國湖北(潛江)龍蝦節”是否和年齡段有關?
(2)現已用分層抽樣的辦法從中老年人中選取了![]() 人進行問卷調查.若再從這
人進行問卷調查.若再從這![]() 人中選取
人中選取![]() 人進行面對面詢問,求事件“選取的
人進行面對面詢問,求事件“選取的![]() 人中恰有
人中恰有![]() 人關注“中國湖北(潛江)龍蝦節””的概率.
人關注“中國湖北(潛江)龍蝦節””的概率.
附:參考公式![]() ,其中
,其中![]() .
.
臨界值表:
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com