
【題目】已知函數![]()
(1)若f(x)在[0,2]上是單調函數,求a的值;
(2)已知對![]() ∈[1,2],f(x)≤1均成立,求a的取值范圍.
∈[1,2],f(x)≤1均成立,求a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據![]() 求導,令
求導,令![]() 解得
解得![]() ,
,![]() ,然后分
,然后分![]()
![]()
![]() 討論求解.
討論求解.
(2)解法一:根據“對![]() ,
,![]() 均成立”,則
均成立”,則![]() 成立,得到
成立,得到![]() ,則
,則![]() 結合(1),
結合(1),![]() 時,
時,![]() ,
,![]() 在
在![]() 上增,將“對
上增,將“對![]() ,
,![]() 均成立”轉化為
均成立”轉化為![]() 求解即可.
求解即可.
(1)因為![]()
所以![]() ,
,
令![]() 解得
解得![]() ,
,![]() .
.
若![]() 即
即![]() ,
,
則![]() 對
對![]() 成立,函數
成立,函數![]() 在
在![]() 上單調,符合題目要求;
上單調,符合題目要求;
若![]() 即
即![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
函數![]() 在
在![]() 上不單調,不符合題目要求;
上不單調,不符合題目要求;
若![]() 即
即![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
函數![]() 在
在![]() 上不單調,不符合題目要求.
上不單調,不符合題目要求.
綜上,若![]() 在
在![]() 上是單調函數,則
上是單調函數,則![]() 取唯一值:
取唯一值:![]() .
.
(2)解法一:已知“對![]() ,
,![]() 均成立”,
均成立”,
取![]() 得
得![]() ,
,
則![]() ,
,![]() ,則
,則![]() 時,
時,![]() ,
,![]() 在
在![]() 上增,
上增,
“對![]() ,
,![]() 均成立”等價于
均成立”等價于![]() ,
,
![]() ,
,
與![]() 取交集,得
取交集,得![]() ,
,
所以![]() 的取值范圍是
的取值范圍是![]()
解法二:根據(1),若![]() ,則
,則![]() 在
在![]() 上單減,
上單減,
“在區間![]() 上,
上,![]() 恒成立”等價于
恒成立”等價于![]()
![]() ,不成立;
,不成立;
若![]() 即
即![]() ,則
,則![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單減,
上單減,
在區間![]() 上,
上,![]() ,“在區間
,“在區間![]() 上,
上,![]() 恒成立”不成立;
恒成立”不成立;
若![]() 即
即![]() ,則
,則![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單增,
上單增,
在區間![]() 上,
上,![]() ,
,
“在區間![]() 上,
上,![]() 恒成立”
恒成立” ![]()
![]() ,
,
解得![]() ,與
,與![]() 相交取交集,得
相交取交集,得![]() ;
;
若![]() 即
即![]() ,則
,則![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
函數![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
在區間![]() 上,
上,![]() ,
,
“在區間![]() 上,
上,![]() 恒成立”
恒成立”![]()
![]() .
.
設![]() ,
,
則![]() ,
,![]() 在
在![]() 上遞增,
上遞增,![]() ,
,
則函數![]() 在
在![]() 上遞增,
上遞增,![]() ,
,
因此![]() 時,
時,![]()
![]() 均不成立.
均不成立.
綜上,所求![]() 的取值范圍是
的取值范圍是![]()


科目:高中數學 來源: 題型:
【題目】在極坐標系中,點![]() 的極坐標是
的極坐標是![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .以極點為坐標原點,極軸為
.以極點為坐標原點,極軸為![]() 軸的正半軸建立平面直角坐標系,斜率為
軸的正半軸建立平面直角坐標系,斜率為![]() 的直線
的直線![]() 經過點
經過點![]() .
.
(1)若![]() 時,寫出直線
時,寫出直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 和曲線
和曲線![]() 相交于不同的兩點
相交于不同的兩點![]() ,求線段
,求線段![]() 的中點
的中點![]() 的在直角坐標系中的軌跡方程.
的在直角坐標系中的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為了研究工人的日平均生產量是否與年齡有關,現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,再將兩組工人的日平均生產件數分成5組: ![]() ,分別加以統計,得到如圖所示的頻率分布直方圖.
,分別加以統計,得到如圖所示的頻率分布直方圖.

(1)根據“25周歲以上組”的頻率分布直方圖,求25周歲以上組工人日平均生產件數的中位數的估計值(四舍五入保留整數);
(2)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的概率;
(3)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“生產能手與工人所在年齡組有關”?
的把握認為“生產能手與工人所在年齡組有關”?
生產能手 | 非生產能手 | 合計 | |
25周歲以上組 | |||
25周歲以下組 | |||
合計 |
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽籺,俗稱“粽子”,古稱“角黍”,是端午節大家都會品嘗的食品,傳說這是為了紀念戰國時期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個邊長為1的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球體積的最大值為____.
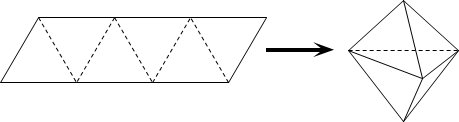
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() .其中
.其中![]() ,
,![]() 表示直線,
表示直線,![]() 、β表示平面,給出如下5個命題:
、β表示平面,給出如下5個命題:
①若![]() //
//![]() ,則
,則![]() //
//![]() ;
;
②若![]() ⊥
⊥![]() ,則
,則![]() ⊥
⊥![]() ;
;
③![]() 與
與![]() 不垂直,則
不垂直,則![]() 不可能成立;
不可能成立;
④若![]() ,則
,則![]() ;
;
⑤![]() ,則
,則![]() ;
;
其中真命題的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市先后采用甲、乙兩種方案治理空氣污染各一年,各自隨機抽取一年(365天)內100天的空氣質量指數API的檢測數據進行分析,若空氣質量指數值在[0,300]內為合格,否則為不合格.表1是甲方案檢測數據樣本的頻數分布表,如圖是乙方案檢測數據樣本的頻率分布直方圖.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天數 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
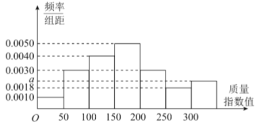
(1)將頻率視為概率,求乙方案樣本的頻率分布直方圖中![]() 的值,以及乙方案樣本的空氣質量不合格天數;
的值,以及乙方案樣本的空氣質量不合格天數;
(2)求乙方案樣木的中位數;
(3)填寫下面2×2列聯表(如表2),并根據列聯表判斷是否有90%的把握認為該城市的空氣質量指數值與兩種方案的選擇有關.
表2:
甲方案 | 乙方案 | 合計 | |
合格天數 | _______ | _______ | _______ |
不合格天數 | _______ | _______ | _______ |
合計 | _______ | _______ | _______ |
附: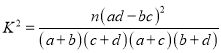
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為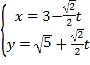 (
(![]() 為參數),在以坐標原點
為參數),在以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸的極坐標中,圓
軸正半軸為極軸的極坐標中,圓![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的坐標為
的坐標為![]() ,圓
,圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的離心率為
的離心率為![]() ,雙曲線
,雙曲線![]() 的漸近線與橢圓
的漸近線與橢圓![]() 的交點到原點的距離均為
的交點到原點的距離均為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 三點共線,直線
三點共線,直線![]() 的斜率分別為
的斜率分別為![]() .
.
(i)證明:![]() ;
;
(ii)若![]() ,設直線
,設直線![]() 過點
過點![]() ,直線
,直線![]() 過點
過點![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,直線
,直線![]() :
:![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)若![]() ,求直線的方程;
,求直線的方程;
(2)過點![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() ,
,![]() 的中點分別為
的中點分別為![]() ,
,![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求點
,求點![]() 到直線
到直線![]() 與
與![]() 距離和的最大值.
距離和的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com