
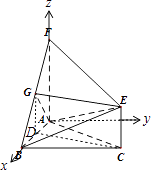
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC.
2CE,G是線段BF上一點,AB=AF=BC. 
(Ⅰ)若EG∥平面ABC,求 ![]() 的值;
的值;
(Ⅱ)求二面角A﹣BF﹣E的大小的正弦值.
【答案】解:(Ⅰ)∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC, AF⊥AC,∴AF⊥平面ABC,則平面ABF⊥平面ABC,
過G作GD⊥AB,垂足為D,則GD⊥平面ABC,連接CD,
由GD⊥平面ABC,AF⊥平面ABC,AF∥CE,可得GD∥CE,
又EG∥平面ABC,∴EG∥CD,則四邊形GDCF為平行四邊形,
∴GD=CE= ![]() ,
,
∴ ![]() =
= ![]() ;
;
(Ⅱ)由(Ⅰ)知AF⊥AB,AF⊥BC
∵BC⊥AB,∴BC⊥平面ABF.
如圖,以A為原點,建立空間直角坐標系A﹣xyz.
則F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1),![]() =(0,2,0)是平面ABF的一個法向量.
=(0,2,0)是平面ABF的一個法向量.
設平面BEF的法向量 ![]() =(x,y,z),則
=(x,y,z),則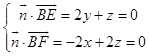 ,令y=1,則z=﹣2,x=﹣2,
,令y=1,則z=﹣2,x=﹣2, ![]() =(﹣2,1,﹣2),
=(﹣2,1,﹣2),
∴cos< ![]() ,
, ![]() >=
>= 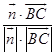 =
= ![]() ,
,
∴二面角A﹣BF﹣E的正弦值為 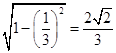 .
.
【解析】(Ⅰ)由平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,可得AF⊥AC,則AF⊥平面ABC,得到平面ABF⊥平面ABC,過G作GD⊥AB,垂足為D,則GD⊥平面ABC,連接CD,可證得則四邊形GDCF為平行四邊形,從而得到GD=CE= ![]() ,則G為BF的中點,得到
,則G為BF的中點,得到 ![]() 的值;(Ⅱ)建立空間直角坐標系,利用向量法即可求二面角E﹣BF﹣A的余弦值.
的值;(Ⅱ)建立空間直角坐標系,利用向量法即可求二面角E﹣BF﹣A的余弦值.
【考點精析】本題主要考查了直線與平面平行的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,已知曲線C的極坐標方程為![]() ,它在點
,它在點![]() 處的切線為直線l.
處的切線為直線l.
(1)求直線l的直角坐標方程;
(2)設直線l與![]() 的交點為P1,P2,求過線段P1P2的中點且與l垂直的直線的極坐標方程.
的交點為P1,P2,求過線段P1P2的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD為正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(Ⅰ)求證:CE∥平面PAD;
(Ⅱ)求PD與平面PCE所成角的正弦值;
(Ⅲ)在棱AB上是否存在一點F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
已知關于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
(1)當![]() 變化時,試求不等式的解集
變化時,試求不等式的解集![]() ;
;
(2)對于不等式的解集![]() ,若滿足
,若滿足![]() (其中
(其中![]() 為整數集). 試探究集合
為整數集). 試探究集合![]() 能否為有限集?若 能,求出使得集合
能否為有限集?若 能,求出使得集合![]() 中元素個數最少的
中元素個數最少的![]() 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合![]() ;若不能,請說明理由.
;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義[x]表示不超過x的最大整數,例如[2.11]=2,[﹣1.39]=﹣2,執行如下圖所示的程序框圖,則輸出m的值為 ( )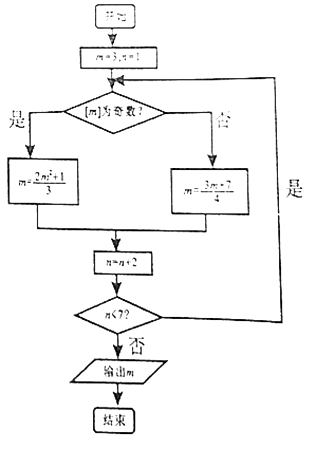
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
已知在直角坐標系xOy中,曲線C的參數方程為 ![]() (φ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為ρcos(θ﹣
(φ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為ρcos(θ﹣ ![]() )=2
)=2 ![]() .
.
(Ⅰ)求曲線C在極坐標系中的方程;
(Ⅱ)求直線l被曲線C截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,數列{bn}是等比數列,Sn是數列{an}的前n項和,a1=b1=1,S2=![]() .
.
(1)若b2是a1,a3的等差中項,求數列{an}與{bn}的通項公式;
(2)若an∈N+,數列{![]() }是公比為9的等比數列,求證:
}是公比為9的等比數列,求證:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,其中m,n,k∈R.
,其中m,n,k∈R.
(1)若m=n=k=1,求f(x)的單調區間;
(2)若n=k=1,且當x≥0時,f(x)≥1總成立,求實數m的取值范圍;
(3)若m>0,n=0,k=1,若f(x)存在兩個極值點x1、x2 , 求證: ![]() <f(x1)+f(x2)<
<f(x1)+f(x2)< ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com