
若橢圓C: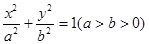 上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2
上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2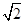 ,△PF1F2s的面積最大值為1
,△PF1F2s的面積最大值為1
(I)求橢圓的方程
(II)若過點M(2,0)的直線l與橢圓C交于不同兩點A、B,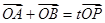 (O為坐標原點)且
(O為坐標原點)且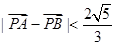 | ,求實數t的取值范圍.
| ,求實數t的取值范圍.
(I)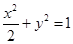 ;
;
(II)t的取值范圍是(-2,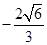 )∪(
)∪(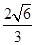 ,2)
,2)
【解析】本試題主要是考查了橢圓方程的求解以及直線與橢圓的位置關系的運用。
(1)因為橢圓C: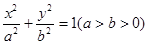 上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2
上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2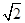 ,△PF1F2s的面積最大值為1
,△PF1F2s的面積最大值為1
利用定義和三角形的面積公式得到a,b,c的值得到橢圓方程。
(2)設出直線方程,然后與橢圓聯立方程組,得到關于變元的二次函數,然后借助于韋達定理和向量的關系式得到參數t與k的關系,然后借助于函數的性質得到范圍。
解:(I)由已知得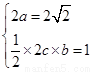
∴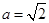 ,
,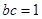 ,又∵
,又∵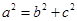 ,∴
,∴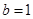 ,
,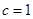
所以橢圓的方程為: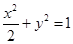
(II)l的斜率必須存在,即設l: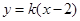
聯立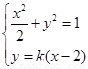 ,消去y得
,消去y得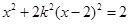
即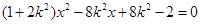
由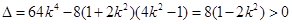 ,得
,得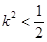
設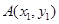 ,
,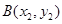 ,由韋達定理得
,由韋達定理得
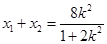 ,
,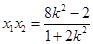
而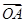 +
+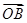 =
=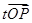 ,設P(x,y),∴
,設P(x,y),∴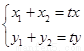
∴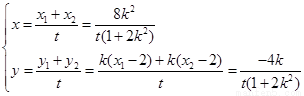
而P在橢圓C上
∴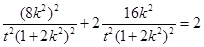 ,∴
,∴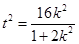 (*)
(*)
又∵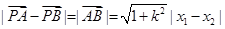
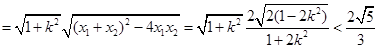
解之,得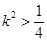 ,∴
,∴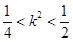
再將(*)式化為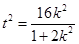
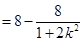 ,將
,將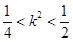 代入
代入
得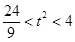 ,即
,即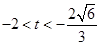 或
或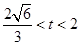
則t的取值范圍是(-2,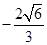 )∪(
)∪(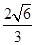 ,2)
,2)


科目:高中數學 來源: 題型:
 (2013•江蘇一模)已知橢圓E:
(2013•江蘇一模)已知橢圓E:| x2 | 4 |
查看答案和解析>>
科目:高中數學 來源:陜西省寶雞中學2012屆高三適應性考試數學文科試題 題型:044
若橢圓C:![]() 上有一動點P,P到橢圓C的兩焦點F1,F2的距離之和等于2
上有一動點P,P到橢圓C的兩焦點F1,F2的距離之和等于2![]() ,△PF1F2的面積最大值為1
,△PF1F2的面積最大值為1
(I)求橢圓的方程
(II)若過點M(2,0)的直線l與橢圓C交于不同兩點A、B,![]() (O為坐標原點)且
(O為坐標原點)且![]() |,求實數t的取值范圍.
|,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年陜西省高三適應性考試文科數學試卷(解析版) 題型:解答題
若橢圓C: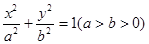 上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2
上有一動點P,P到橢圓C的兩焦點 F1,F2的距離之和等于2 ,△PF1F2的面積最大值為1
,△PF1F2的面積最大值為1
(I)求橢圓的方程
(II)若過點M(2,0)的直線l與橢圓C交于不同兩點A、B,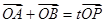 (O為坐標原點)且
(O為坐標原點)且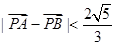 | ,求實數t的取值范圍.
| ,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013年江蘇省蘇錫常鎮、徐州、連云港六市高考數學一模試卷(解析版) 題型:解答題
 的左、右頂點分別為A,B,圓x2+y2=4上有一動點P,P在x軸的上方,C(1,0),直線PA交橢圓E于點D,連結DC,PB.
的左、右頂點分別為A,B,圓x2+y2=4上有一動點P,P在x軸的上方,C(1,0),直線PA交橢圓E于點D,連結DC,PB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com