
已知函數 的圖象在
的圖象在 上連續,定義:
上連續,定義: ,
,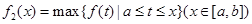 .其中,
.其中, 表示函數
表示函數 在
在 上的最小值,
上的最小值, 表示函數
表示函數 在
在 上的最大值.若存在最小正整數
上的最大值.若存在最小正整數 ,使得
,使得 對任意的
對任意的 成立,則稱函數
成立,則稱函數 為
為 上的“
上的“ 階收縮函數”.
階收縮函數”.
(Ⅰ)若 ,試寫出
,試寫出 ,
, 的表達式;
的表達式;
(Ⅱ)已知函數 ,試判斷
,試判斷 是否為
是否為 上的“
上的“ 階收縮函數”.如果是,求出對應的
階收縮函數”.如果是,求出對應的 ;如果不是,請說明理由;
;如果不是,請說明理由;
(Ⅲ)已知 ,函數
,函數 是
是 上的2階收縮函數,求
上的2階收縮函數,求 的取值范圍.
的取值范圍.
(Ⅰ)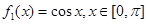 ,
,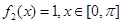 ;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4階收縮函數.(Ⅲ)
;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4階收縮函數.(Ⅲ)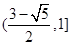
解析試題分析:(Ⅰ)根據f(x)=cosx的最大值為1,可得f1(x)、f2(x)的解析式.
(Ⅱ)根據函數f(x)=x2在x∈[-1,4]上的值域,先寫出f1(x)、f2(x)的解析式,再由f2(x)-f1(x)≤k(x-a)求出k的范圍得到答案.
(3)先對函數f(x)進行求導判斷函數的單調性,進而寫出f1(x)、f2(x)的解析式,
然后再由f2(x)-f1(x)≤k(x-a)求出k的范圍得到答案.
試題解析:
(Ⅰ)由題意可得: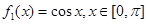 ,
,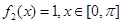 2分
2分
(Ⅱ)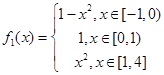 ,
,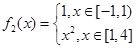 ,
,
所以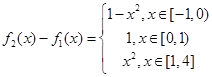 4分
4分
當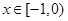 時,
時,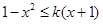 ,∴
,∴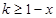 ,即
,即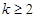 ;
;
當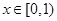 時,
時,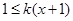 ,∴
,∴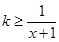 ,即
,即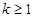 ;
;
當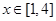 時,
時,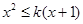 ,∴
,∴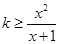 ,即
,即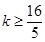 .
.
綜上所述,∴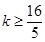
即存在k=4,使得f(x)是[﹣1,4]上的4階收縮函數. 7分
(Ⅲ)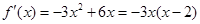 令
令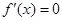 得
得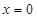 或
或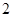 .函數f(x)的變化情況如下:
.函數f(x)的變化情況如下: