
(12分)定義在區(qū)間(-1,1)上的函數(shù)f (x)滿足:①對任意的x,y∈(-1,1),都有f (x)
+ f (y) =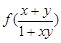 ; ②當(dāng)x∈(-1,0),f (x) > 0.
; ②當(dāng)x∈(-1,0),f (x) > 0.
(1)求證f (x)為奇函數(shù);
(2)試解不等式:f (x) + f (x-1)  .
.
(1)略
(2)不等式的解集為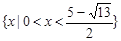
【解析】解:(1)解:令x = y = 0,則
f (0) + f
(0) = 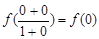 ∴ f (0) = 0
∴ f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴ f (x) + f (-x) = f (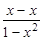 ) = f (0) = 0
) = f (0) = 0
∴ f (-x) =-f (x)
∴ f (x) 在(-1,1)上為奇函數(shù)…………………4分
(2)解:令-1< x1 < x2 < 1
則f (x1) -f (x2) = f (x1) + f
(-x2) = 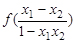
∵x1-x2 < 0,1-x1x2 > 0
∴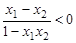 ∴
∴ 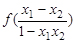 > 0
> 0
∴ f (x1) > f (x2) ∴ f (x) 在(-1,1)上為減函數(shù)
又f (x) + f (x-1) >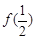
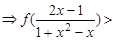
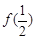 …………………8分
…………………8分
∴ 不等式化為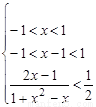
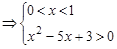
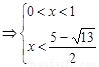 或
或
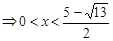
∴ 不等式的解集為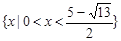 …………………12分
…………………12分


 100分闖關(guān)期末沖刺系列答案
100分闖關(guān)期末沖刺系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| f(a)+f(b) | a+b |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
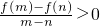
 )+f(x-1)<0,求x的取值范圍
)+f(x-1)<0,求x的取值范圍查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(ⅰ)f(-1)=f(1)=0;
(ⅱ)對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.
(Ⅰ)證明:對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(Ⅱ)證明:對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1;
(Ⅲ)在區(qū)間[-1,1]上是否存在滿足題設(shè)條件的函數(shù)y=f(x),且使得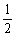
若存在,請舉一例;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(ⅰ)f(-1)=f(1)=0;
(ⅱ)對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.
(Ⅰ)證明:對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(Ⅱ)判斷函數(shù)g(x)=![]() ,是否滿足題設(shè)條件;
,是否滿足題設(shè)條件;
(Ⅲ)在區(qū)間[-1,1]上是否存在滿足題設(shè)條件的函數(shù)y=f(x),且使得對任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|.
若存在,請舉一例;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年安徽省安慶市望江中學(xué)高三(上)第一次月考數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
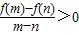
 )+f(x-1)<0,求x的取值范圍
)+f(x-1)<0,求x的取值范圍查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com