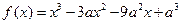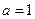.
，求函數(shù)
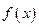的極值；
，且當(dāng)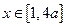
時(shí)，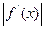
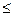12a恒成立，試確定
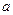的取值范圍.
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
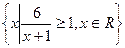，B＝{x|x2－2x－m<0}，查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
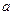是實(shí)數(shù)，設(shè)函數(shù)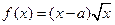
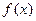的單調(diào)性；
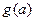為函數(shù)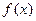在區(qū)間
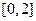上的最小值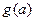的表達(dá)式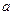；的取值范圍，使得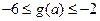
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
，
．
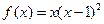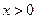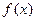的極值；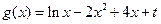
（
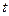為常數(shù)），若使
≤
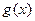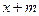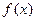≤在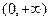
上恒成立的實(shí)數(shù)
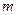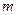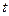有且只有一個(gè)，求實(shí)數(shù)和的值；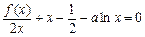
的解的個(gè)數(shù)，并說明理由.查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
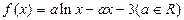
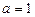時(shí)，求函數(shù)
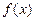的單調(diào)區(qū)間；
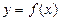的圖像在點(diǎn)
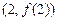處的切線的傾斜角為
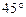，問：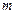
在什么范圍取值時(shí)，函數(shù)
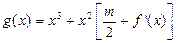在區(qū)間
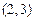上總存在極值？查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：單選題
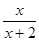在點(diǎn)(－1，－1)處的切線方程為(......)| A．y＝2x＋1 ........................ | B．y＝2x－1 |
| C．y＝－2x－3 .................. | D．y＝－2x－2 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
求導(dǎo)數(shù)，得21 
[
列表討論
的變化情況：
，極小值是
7分
的圖像是一條開口向上的拋物線，關(guān)于x=a對(duì)稱.
上是增函數(shù)，從而 
上的最小值是
最大值是
于是有 
不恒成立.
恒成立的a的取值范圍是
．若過點(diǎn)
可作曲線
的切線有三條，求實(shí)數(shù)
的取值范圍．
，在
上最小值為
，最大值為
，求
的值．