
【題目】某校高二理科8班共有50名學生參加學業水平模擬考試,成績(單位:分,滿分100分)大于或等于90分的為優秀,其中語文成績近似服從正態分布![]() ,數學成績的頻率分布直方圖如圖.
,數學成績的頻率分布直方圖如圖.
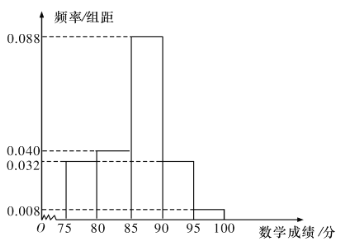
(I)這50名學生中本次考試語文、數學成績優秀的大約各有多少人?
(Ⅱ)如果語文和數學兩科成績都優秀的共有4人,從語文優秀或數學優秀的這些同學中隨機抽取3人,設3人中兩科都優秀的有![]() 人,求
人,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)根據(I)(Ⅱ)的數據,是否有99%以上的把握認為語文成績優秀的同學,數學成績也優秀?
附:①若![]() ~
~![]() ,則
,則![]() ,
,![]() ;
;
②![]() ;
;
③
【答案】(Ⅰ) 語文成績優秀的同學有8人,數學成績優秀的同學有10人. (Ⅱ)見解析.( Ⅲ) 沒有99%以上的把握認為語文成績優秀的同學,數學成績也優秀.
【解析】
(I)語文成績服從正態分布,根據正態分布的![]() 原則可得語文成績優秀的概率及人數;根據數學成績的頻率分布直方圖可以計算數學成績優秀的概率及人數;(Ⅱ)語文和數學兩科成績都優秀的共有4人,則語文單科優秀的4人,數學單科優秀的6人,即單科優秀的共10人,隨機抽取3人,3人中兩科都優秀的可能為0、1、2、3四種情況,服從超幾何分布,利用概率公式分別求出每種情況的概率,即可寫出X的分布列及數學期望;(Ⅲ)先填寫列聯表,利用公式求出
原則可得語文成績優秀的概率及人數;根據數學成績的頻率分布直方圖可以計算數學成績優秀的概率及人數;(Ⅱ)語文和數學兩科成績都優秀的共有4人,則語文單科優秀的4人,數學單科優秀的6人,即單科優秀的共10人,隨機抽取3人,3人中兩科都優秀的可能為0、1、2、3四種情況,服從超幾何分布,利用概率公式分別求出每種情況的概率,即可寫出X的分布列及數學期望;(Ⅲ)先填寫列聯表,利用公式求出![]() 的值比較它與6.635的大小即可。
的值比較它與6.635的大小即可。
(Ⅰ)∵語文成績服從正態分布![]() ,
,
∴語文成績優秀的概率為![]() ,
,
數學成績優秀的概率為![]() ,
,
∴語文成績優秀的同學有![]() 人,
人,
數學成績優秀的同學有![]() 人.
人.
(Ⅱ)語文數學兩科都優秀的有4人,單科優秀的有10人,
![]() 的所有可能取值為0,1,2,3,
的所有可能取值為0,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 的分布列為:
的分布列為:
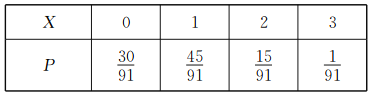
![]() .
.
(Ⅲ)![]() 列聯表:
列聯表:
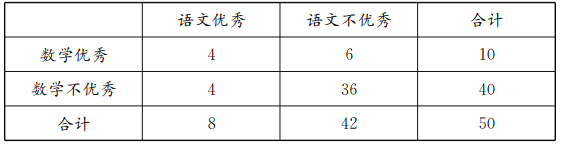
∴![]() .
.
∴沒有99%以上的把握認為語文成績優秀的同學,數學成績也優秀.


科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱錐![]() 中,
中,![]() 與
與![]() 都是邊長為2的等邊三角形,
都是邊長為2的等邊三角形,![]() 是側棱
是側棱![]() 的中點,過點
的中點,過點![]() 作平行于
作平行于![]() 、
、![]() 的平面分別交棱
的平面分別交棱![]() 、
、![]() 、
、![]() 于點
于點![]() 、
、![]() 、
、![]() .
.
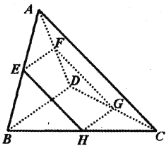
(1)證明:四邊形![]() 為矩形;
為矩形;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個工廠在某年連續10個月每月產品的總成本y(萬元)與該月產量x(萬件)之間有如下一組數據:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通過畫散點圖,發現可用線性回歸模型擬合y與x的關系,請用相關系數加以說明;
(2)①建立月總成本y與月產量x之間的回歸方程;
②通過建立的y關于x的回歸方程,估計某月產量為1.98萬件時,此時產品的總成本為多少萬元?
(均精確到0.001)
附注:①參考數據:![]() ,
,
![]() ,
,
②參考公式:相關系數 ,
,
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 是梯形,四邊形
是梯形,四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上的動點.
上的動點.
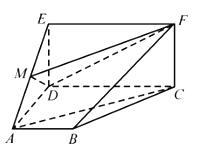
(1)試確定點![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)在(1)的條件下,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】武漢市攝影協會準備在2020年1月舉辦主題為“我們都是追夢人”攝影圖片展,通過平常人的鏡頭記錄國強民富的幸福生活,攝影協會收到了來自社會各界的大量作品,打算從眾多照片中選取100張照片展出,其參賽者年齡集中![]() 在之間,根據統計結果,做出頻率分布直方圖如圖:
在之間,根據統計結果,做出頻率分布直方圖如圖:

(1)求頻率直方圖中![]() 的值,并根據頻率直方圖,求這100位攝影者年齡的中位數;
的值,并根據頻率直方圖,求這100位攝影者年齡的中位數;
(2)為了展示不同年齡作者眼中的幸福生活,攝影協會按照分層抽樣的方法,計劃從這100件照片中抽出20個最佳作品,并邀請相應作者參加“講述照片背后的故事”座談會.
①在答題卡上的統計表中填出每組相應抽取的人數:
年齡 |
|
|
|
|
|
人數 |
②若從年齡在![]() 的作者中選出2人把這些圖片和故事整理成冊,求這2人中至少有1人的年齡在
的作者中選出2人把這些圖片和故事整理成冊,求這2人中至少有1人的年齡在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求證:數列{an-1}是等比數列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果對任意n∈N*,都有bn+![]() t≤t2,求實數t的取值范圍.
t≤t2,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線;
處的切線;
(2)若函數![]() 在其定義域內為增函數,求正實數
在其定義域內為增函數,求正實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com