【題目】已知圓
過
， 
兩點，且圓心
在直線
上.
（1）求圓
的方程；
（2）若直線
過點
且被圓
截得的線段長為
，求
的方程.
【答案】（1）
；（2）
或
【解析】試題分析：（1）把點P、Q的坐標和圓心坐標代入圓的一般方程，利用待定系數法求得系數的值；（2）分類討論，斜率存在和斜率不存在兩種情況．①當直線l的斜率不存在時，滿足題意，易得直線方程；②當直線l的斜率存在時，設所求直線l的斜率為k，則直線l的方程為：y-5=kx，由點到直線的距離公式求得k的值．
試題解析：
（1）設圓的方程為
，圓心
，根據題意有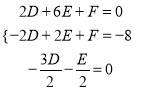
，計算得出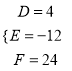
，
故所求圓的方程為
.
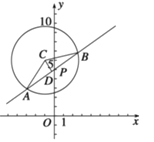
（2）如圖所示， 
，設
是線段
的中點，
則
，
∴
， 
.
在
中，可得
.
當直線
的斜率不存在時，滿足題意，
此時方程為
.
當直線
的斜率存在時，設所求直線
的斜率為
，則直線
的方程為： 
，
即
，由點
到直線
的距離公式：
，得
，此時直線
的方程為
.
∴所求直線
的方程為
或
開心蛙狀元作業系列答案
課時掌控隨堂練習系列答案
一課一練一本通系列答案
浙江之星學業水平測試系列答案科目：高中數學 來源： 題型：
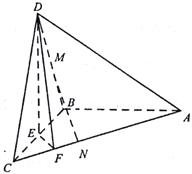
【題目】如圖,在三棱錐D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC的中點,F在棱AC上,且AF=3FC
(1)求三棱錐D-ABC的體積
(2)求證:平面DAC⊥平面DEF;
(3)若M為DB中點,N在棱AC上,且CN=
CA,求證:MN∥平面DEF
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了準確地把握市場，做好產品生產計劃，對過去四年的數據進行整理得到了第
年與年銷量
（單位：萬件）之間的關系如下表：
（1）在圖中畫出表中數據的散點圖；
（2）根據散點圖選擇合適的回歸模型擬合
與
的關系（不必說明理由）；
（3）建立
關于
的回歸方程，預測第5年的銷售量.
附注：參考公式：回歸直線的斜率和截距的最小二乘法估計公式分別為：
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
中，底面
為正三角形， 
底面
，且
， 
是
的中點.
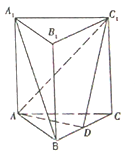
（1）求證： 
平面
；
（2）求證：平面
平面
；
（3）在側棱
上是否存在一點
，使得三棱錐
的體積是
？若存在，求出
的長；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一條生產線上按同樣的方式每隔30分鐘取一件產品，共取了n件，測得其產品尺寸后，畫得其頻率分布直方圖如圖所示，已知尺寸在[15，45）內的頻數為46．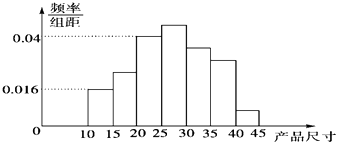 
（1）該抽樣方法是什么方法？
（2）求n的值；
（3）求尺寸在[20，25）內的產品的件數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
