
【題目】已知函數![]() ,函數
,函數![]() .
.
(1)若函數![]() ,
, ![]() 的最小值為-16,求實數
的最小值為-16,求實數![]() 的值;
的值;
(2)若函數![]() 在區間
在區間![]() 上是單調減函數,求實數
上是單調減函數,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)8或-32;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】試題分析:(1)設![]() ,由
,由![]() ,可得
,可得![]() ,化簡
,化簡![]() 得
得![]() ,
, ![]() ,根據對稱軸與
,根據對稱軸與![]() 的關系,求出函數的最小值可得實數
的關系,求出函數的最小值可得實數![]() 的值;(2)由函數
的值;(2)由函數![]() 的圖象知:函數的減區間為
的圖象知:函數的減區間為![]() ,
, ![]() ,則
,則![]() 或
或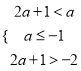 ,由此可得實數
,由此可得實數![]() 的取值范圍;(3)不等式
的取值范圍;(3)不等式![]() 可以化為
可以化為![]() ,即
,即![]() ,則問題轉化為當
,則問題轉化為當![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,令
,令![]() (
(![]() ),討論函數
),討論函數![]() 的單調性和最小值,即可求實數
的單調性和最小值,即可求實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)設![]() ,又
,又![]() ,則
,則![]() ,
,
化簡得![]() ,
, ![]() ,對稱軸方程為
,對稱軸方程為![]() ,
,
當![]() ,即
,即![]() 時,有
時,有![]() ,解得
,解得![]() 或
或![]() ;
;
當![]() ,即
,即![]() 時,有
時,有![]() ,解得
,解得![]() (舍);
(舍);
所以實數![]() 的值為8或-32;
的值為8或-32;
(2)由函數![]() 的圖象知:函數的減區間為
的圖象知:函數的減區間為![]() ,
, ![]() ,
,
![]()
![]()
![]() 或
或![]()
![]()
![]() ,則
,則![]() 或
或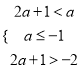 ;
;
則實數![]() 的取值范圍為
的取值范圍為![]() 或
或![]()
(3)不等式![]() 可以化為
可以化為![]() ,即
,即![]() ,
,
因為當![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,
,
所以當![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,
,
令![]() (
(![]() ),則函數
),則函數![]() 在區間
在區間![]() 上單調增函數,在
上單調增函數,在![]() 上單調減函數,所以
上單調減函數,所以![]() ,所以
,所以![]() ,從而
,從而![]() ,即所求實數
,即所求實數![]() 的取值范圍
的取值范圍![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E、F分別是BB1、CD的中點.
(1)求證:平面AED⊥平面A1FD1;
(2)在AE上求一點M,使得A1M⊥平面ADE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸建立極坐標系.
(1)將直線l:  (t為參數)化為極坐標方程;
(t為參數)化為極坐標方程;
(2)設P是(1)中直線l上的動點,定點A( ![]() ,
, ![]() ),B是曲線ρ=﹣2sinθ上的動點,求|PA|+|PB|的最小值.
),B是曲線ρ=﹣2sinθ上的動點,求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 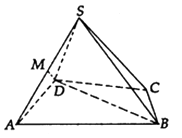
(1)求證:SA⊥BD;
(2)若∠BCD=120°,M為棱SA的中點,求證:DM∥平面SBC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]()
(Ⅰ)求函數![]() 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(Ⅱ)當![]() 時,方程
時,方程![]() 恰有兩個不同的實數根,求實數
恰有兩個不同的實數根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)將函數![]() 的圖象向右平移
的圖象向右平移![]() (
(![]() )個單位后所得函數
)個單位后所得函數![]() 的圖象關于原點中心對稱,求
的圖象關于原點中心對稱,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=xlnx+ax,a∈R.
(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若對x>1,f(x)>(b+a﹣1)x﹣b恒成立,求整數b的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓M恒過點(0,1),且與直線y=﹣1相切.
(1)求圓心M的軌跡方程;
(2)動直線l過點P(0,﹣2),且與點M的軌跡交于A、B兩點,點C與點B關于y軸對稱,求證:直線AC恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為奇函數,
為奇函數, ![]() 為偶函數,且
為偶函數,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定義域;
的解析式及定義域;
(2)若關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
(3)如果函數![]() ,若函數
,若函數![]() 有兩個零點,求實數
有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com