【題目】某工廠擬造一座平面為長方形，面積為
的三級污水處理池.由于地形限制，長、寬都不能超過
，處理池的高度一定.如果池的四周墻壁的造價為
元
，中間兩道隔墻的造價為
元
，池底的造價為
元
，則水池的長、寬分別為多少米時，污水池的造價最低？最低造價為多少元？
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系中，以坐標原點為極點， 
軸的正半軸與極軸建立極坐標系，已知曲線
的極坐標方程為
，過點
且傾斜角為
的直線
與曲線
相交于
兩點.
（1）寫出曲線
的直角坐標方程和直線
的普通方程；
（2）若
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在長方體ABCD﹣A1B1C1D1中，AB=
， BC=AA1=1，點M為AB1的中點，點P為對角線AC1上的動點，點Q為底面ABCD上的動點（點P、Q可以重合），則MP+PQ的最小值為（ ）
A.
B.
C.
D.1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】濰坊文化藝術中心的觀光塔是濰坊市的標志性建筑，某班同學準備測量觀光塔
的高度
（單位：米），如圖所示，垂直放置的標桿
的高度
米，已知
， 
.
（1）該班同學測得
一組數據： 
，請據此算出
的值；
（2）該班同學分析若干測得的數據后，發現適當調整標桿到觀光塔的距離
（單位：米），使
與
的差較大，可以提高測量精確度，若觀光塔高度為136米，問
為多大時， 
的值最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠擬造一座平面為長方形，面積為
的三級污水處理池.由于地形限制，長、寬都不能超過
，處理池的高度一定.如果池的四周墻壁的造價為
元
，中間兩道隔墻的造價為
元
，池底的造價為
元
，則水池的長、寬分別為多少米時，污水池的造價最低？最低造價為多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為選拔選手參加“中國謎語大會”，某中學舉行了一次“謎語大賽”活動．為了了解本次競賽學生的成績情況，從中抽取了部分學生的分數（得分取正整數，滿分為100分）作為樣本（樣本容量為
）進行統計．按照
， 
， 
， 
的分組作出頻率分布直方圖，并作出樣本分數的莖葉圖（圖中僅列出了得分在
， 
的數據）．
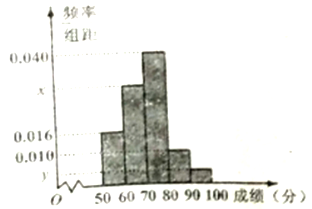
（Ⅰ）求樣本容量
和頻率分布直方圖中的
， 
的值；
（Ⅱ）分數在
的學生設為一等獎，獲獎學金500元；分數在
的學生設為二等獎，獲獎學金200元．已知在樣本中，獲一、二等獎的學生中各有一名男生，則從剩下的女生中任取三人，求獎學金之和大于600的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=log4（4x+1）+kx（k∈R）是偶函數．
（1）求實數k的值；
（2）設g（x）=log4（a2x+a），若f（x）=g（x）有且只有一個實數解，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=4x﹣2x+1+3，當x∈[﹣2，1]時，f（x）的最大值為m，最小值為n，
（1）若角α的終邊經過點P（m，n），求sinα+cosα的值；
（2）g（x）=mcos（nx+
）+n，求g（x）的最大值及自變量x的取值集合．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
