已知定義域為[0,1]的函數f(x)同時滿足以下三個條件:
(1)對任意的x∈[0,1],總有f(x)>0;
(2)f(1)=1;
(3)若x1≥0,x2≥0,x1+x2≤1,則有f(x1+x2)≥f(x1)+f(x2)成立,則稱f(x)為“友誼函數”,請解答下列各題:
①若已知f(x)為“友誼函數”,求f(0)的值并判斷函數的單調性;
②函數g(x)=2x-1在區間[0,1]上是否為“友誼函數”?并給出理由.
解:①取x
1=x
2=0,代入f(x
1+x
2)≥f(x
1)+f(x
2),
得f(0)≥f(0)+f(0),化簡可得f(0)≤0
又由f(0)≥0,得f(0)=0
設0≤x
1<x
2≤1,則0<x
2-x
1<1,
所以f(x
2)=f(x
2-x
1+x
1)≥f(x
2-x
1)+f(x
1)≥f(x
1)
故有f(x
1)≤f(x
2),故函數f(x)為定義在[0,1]上的增函數;
②顯然g(x)=2
x-1在[0,1]上滿足(1)g(x)>0;(2)g(1)=1;(3)若x
1≥0,x
2≥0,且x
1+x
2≤1,則有
g(x
1+x
2)-[g(x
1)+g(x
2)]=
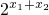
-1-[(

-1)+(

-1)]=(

-1)(

-1)≥0
故g(x)=2
x-1滿足條件(1)、(2)、(3),
所以g(x)=2
x-1為友誼函數.
分析:①賦值可考慮取x
1=x
2=0,代入f(x
1+x
2)≥f(x
1)+f(x
2),可得f(0)≥f(0)+f(0),由已知f(0)≥0,可得f(0)=0,由0≤x
1<x
2≤1,則0<x
2-x
1<1,故有f(x
2)=f(x
2-x
1+x
1)≥f(x
2-x
1)+f(x
1)≥f(x
1),即得結論成立;
②要判斷函數g(x)=2
x-1在區間[0,1]上是否為“友誼函數,只要檢驗函數g(x)=2
x-1在[0,1]上是否滿足(1)g(x)>0;(2)g(1)=1;(3)x
1≥0,x
2≥0,且x
1+x
2≤1,有g(x
1+x
2)≥g(x
1)+g(x
2)即可.
點評:采用賦值法是解決抽象函數的性質應用的常用方法,而函數的新定義往往轉化為一般函數性質的研究,本題結合指數函數的性質研究函數的函數的函數值域的應用,指數函數的單調性的應用.

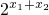 -1-[(
-1-[( -1)+(
-1)+( -1)]=(
-1)]=( -1)(
-1)( -1)≥0
-1)≥0
