
【題目】已知函數(shù)![]() .
.
(1)若![]() 是
是![]() 的極小值點,求實數(shù)
的極小值點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
【答案】(1)![]() ;(2)證明見解析
;(2)證明見解析
【解析】
(1)求得![]() 的定義域,并求導,利用分類討論當
的定義域,并求導,利用分類討論當![]() 時,分析單調(diào)性顯然成立;當
時,分析單調(diào)性顯然成立;當![]() 時,令
時,令![]() ,得
,得![]() 或
或![]() ,再利用分類討論兩根的大小,分別分析單調(diào)性討論是否成立,得到當
,再利用分類討論兩根的大小,分別分析單調(diào)性討論是否成立,得到當![]() 時成立,當
時成立,當![]() 時與當
時與當![]() 時,都不成立,最后綜上得參數(shù)的取值范圍;
時,都不成立,最后綜上得參數(shù)的取值范圍;
(2)由(1)可知當![]() 時,得
時,得![]() 的單調(diào)性,從而表示
的單調(diào)性,從而表示![]() ;將所證不等式等價轉化為不等式
;將所證不等式等價轉化為不等式![]() 對任意的
對任意的![]() 都恒成立,構建
都恒成立,構建![]() ,利用導數(shù)求得值域
,利用導數(shù)求得值域![]() ,最后由不等式的性質(zhì)即可得證原不等式成立.
,最后由不等式的性質(zhì)即可得證原不等式成立.
(1)![]() 的定義域為
的定義域為![]() ,
,![]()
①當![]() 時,
時,![]() ,則
,則![]() ,
,
令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
此時![]() 是
是![]() 的極小值點,符合題意;
的極小值點,符合題意;
②當![]() 時,令
時,令![]() ,得
,得![]() 或
或![]() .
.
(i)當![]() 時,則
時,則![]() ,
,
所以當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
此時![]() 是
是![]() 的極小值點,符合題意;
的極小值點,符合題意;
(ii)當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() 不是
不是![]() 的極值點.
的極值點.
(iii)當![]() 時,則
時,則![]() ,
,
所以當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增;當
上單調(diào)遞增;當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
此時![]() 是
是![]() 的極大值點,不符合題意.
的極大值點,不符合題意.
綜合①②,得![]() .
.
(2)證明:由(1)可知當![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
又![]() ,所以當
,所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以當![]() 或
或![]() 時,都有
時,都有![]() .
.
要證不等式![]() 對任意的
對任意的![]() 都恒成立,
都恒成立,
即證不等式![]() 對任意的
對任意的![]() 都恒成立,
都恒成立,
設![]() ,則
,則![]() .
.
設![]() ,
,![]() 且
且![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
所以方程![]() 的唯一解為
的唯一解為![]() ,
,
所以當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減;
上單調(diào)遞減;
所以當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() 對任意
對任意![]() 都恒成立.
都恒成立.
所以當![]() 時,不等式
時,不等式![]() 對任意
對任意![]() 都恒成立.
都恒成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程是
的參數(shù)方程是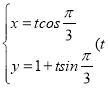 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程是
的參數(shù)方程是 為參數(shù)),以
為參數(shù)),以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求直線![]() 和曲線
和曲線![]() 的極坐標方程;
的極坐標方程;
(2)已知射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,射線
兩點,射線![]() 與直線
與直線![]() 交于
交于![]() 點,若
點,若![]() 的面積為1,求
的面積為1,求![]() 的值和弦長
的值和弦長![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某射擊小組有甲、乙、丙三名射手,已知甲擊中目標的概率是![]() ,甲、丙二人都沒有擊中目標的概率是
,甲、丙二人都沒有擊中目標的概率是![]() ,乙、丙二人都擊中目標的概率是
,乙、丙二人都擊中目標的概率是![]() .甲乙丙是否擊中目標相互獨立.
.甲乙丙是否擊中目標相互獨立.
(1)求乙、丙二人各自擊中目標的概率;
(2)設乙、丙二人中擊中目標的人數(shù)為X,求X的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 為拋物線
為拋物線![]() 上不同的兩點,且
上不同的兩點,且![]() ,點
,點![]()
![]() 且
且![]() 于點
于點![]() .
.
(1)求![]() 的值;
的值;
(2)過![]() 軸上一點
軸上一點 ![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 在
在![]() 的準線上的射影分別為
的準線上的射影分別為![]() ,
,![]() 為
為![]() 的焦點,若
的焦點,若![]() ,求
,求![]() 中點
中點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
(1)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當![]() 時,令
時,令![]() ,是否存在區(qū)間
,是否存在區(qū)間![]() ,使得函數(shù)
,使得函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的值域為
上的值域為![]() ,若存在,求實數(shù)
,若存在,求實數(shù)![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】10名象棋選手進行單循環(huán)賽(即每兩名選手比賽一場).規(guī)定兩人對局勝者得2分,平局各得1分,負者得0分,并按總得分由高到低進行排序.比賽結束后,10名選手的得分各不相同,且第二名的得分是最后五名選手得分之和的![]() .則第二名選手的得分是____.
.則第二名選手的得分是____.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知菱形ABCD中,∠BAD=60°,AC與BD相交于點O.將△ABD沿BD折起,使頂點A至點M,在折起的過程中,下列結論正確的是( )
A.BD⊥CM
B.存在一個位置,使△CDM為等邊三角形
C.DM與BC不可能垂直
D.直線DM與平面BCD所成的角的最大值為60°
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著計算機的出現(xiàn),圖標被賦予了新的含義,又有了新的用武之地.在計算機應用領域,圖標成了具有明確指代含義的計算機圖形.如圖所示的圖標是一種被稱之為“黑白太陽”的圖標,該圖標共分為3部分.第一部分為外部的八個全等的矩形,每一個矩形的長為3、寬為1;第二部分為圓環(huán)部分,大圓半徑為3,小圓半徑為2;第三部分為圓環(huán)內(nèi)部的白色區(qū)域.在整個“黑白太陽”圖標中隨機取一點,則此點取自圖標第三部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com