
【題目】已知拋物線C:y2=2px(p>0)過點M(m,2),其焦點為F,且|MF|=2.
(Ⅰ)求拋物線C的方程;
(Ⅱ)設E為y軸上異于原點的任意一點,過點E作不經過原點的兩條直線分別與拋物線C和圓F:(x﹣1)2+y2=1相切,切點分別為A,B,求證:直線AB過定點F(1,0).
【答案】解:(Ⅰ)拋物線C的準線方程為: ![]() ,
,
∴ ![]() ,
,
又M在拋物線上,
即 ![]() ,
,
∴p2﹣4p+4=0,
解得p=2;
所以拋物線C的方程為y2=4x;
(Ⅱ)設點E(0,t)(t≠0),
由已知切線不為y軸,設EA:y=kx+t,
聯立 ![]() ,消去y,
,消去y,
可得k2x2+(2kt﹣4)x+t2=0;
直線EA與拋物線C相切,
∴△=(2kt﹣4)2﹣4k2t2=0,
即kt=1代入 ![]() ,
,
∴x=t2 , 即A(t2 , 2t);
設切點B(x0 , y0),則由幾何性質可以判斷點O,B關于直線EF:y=﹣tx+t對稱,
則 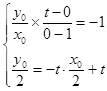 ,
,
解得:  ,
,
即 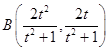 ;
;
思路1:直線AB的斜率為 ![]() ,
,
直線AB的方程為 ![]() ,
,
整理 ![]() ,
,
∴直線AB過定點恒過定點F(1,0);
當t=±1時,A(1,±2),B(1,±1),此時直線AB為x=1,過點F(1,0);
綜上,直線AB過定點恒過定點F(1,0),
思路2:直線AF的斜率為 ![]() ,
,
直線BF的斜率為 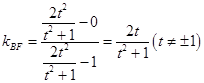 ,
,
∴kAF=kBF , 即A,B,F三點共線;
當t=±1時,A(1,±2),B(1,±1),此時A,B,F共線;
∴直線AB過定點F
【解析】(Ⅰ)根據拋物線的準線方程與M在拋物線上,列出方程組求出p的值即得拋物線方程;(Ⅱ)根據直線EA與圓錐曲線相切,用直線方程與圓錐曲線方程聯立,△=0,根據圓的對稱性,寫出直線AB的方程;
思路1:利用直線AB的斜率、直線AB的方程,判斷直線AB恒過定點;
思路2:根據三點共線以及直線的斜率,判斷直線AB過定點F.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,若滿足①
,若滿足① ![]() ;② 當
;② 當![]() ,且
,且![]() 時,都有
時,都有![]() ;③ 當
;③ 當![]() ,且
,且![]() 時,都有
時,都有![]() ,則稱
,則稱![]() 為“偏對稱函數”.現給出四個函數:①
為“偏對稱函數”.現給出四個函數:①![]() ;②
;② ![]() ; ③
; ③![]() ;④
;④![]() .則其中是“偏對稱函數”的函數序號為 _______.
.則其中是“偏對稱函數”的函數序號為 _______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為比較甲、乙兩地某月11時的氣溫情況,隨機選取該月中的5天中11時的氣溫數據(單位:℃)制成如圖所示的莖葉圖,考慮以下結論:
①甲地該月11時的平均氣溫低于乙地該月11時的平均氣溫
②甲地該月11時的平均氣溫高于乙地該月11時的平均氣溫
③甲地該月11時的氣溫的標準差小于乙地該月11時的氣溫的標準差
④甲地該月11時的氣溫的標準差大于乙地該月11時的氣溫的標準差
其中根據莖葉圖能得到的正確結論的編號為( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有![]() 、
、![]() 兩個崗位招聘大學畢業生,其中第一天收到這兩個崗位投簡歷的大學生人數如下表:
兩個崗位招聘大學畢業生,其中第一天收到這兩個崗位投簡歷的大學生人數如下表:
|
| 總計 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
總計 | 36 | 64 | 100 |
(1)根據以上數據判斷是有![]() 的把握認為招聘的
的把握認為招聘的![]() 、
、![]() 兩個崗位與性別有關?
兩個崗位與性別有關?
(2)從投簡歷的女生中隨機抽取兩人,記其中投![]() 崗位的人數為
崗位的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式:![]() ,其中
,其中![]() .
.
參考數據:
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現從某醫院中隨機抽取了![]() 位醫護人員的關愛患者考核分數(患者考核:
位醫護人員的關愛患者考核分數(患者考核:![]() 分制),用相關的特征量
分制),用相關的特征量![]() 表示;醫護專業知識考核分數(試卷考試:
表示;醫護專業知識考核分數(試卷考試:![]() 分制),用相關的特征量
分制),用相關的特征量![]() 表示,數據如下表:
表示,數據如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 關于
關于![]() 的線性回歸方程(計算結果精確到
的線性回歸方程(計算結果精確到![]() );
);
(2)利用(1)中的線性回歸方程,分析醫護專業考核分數的變化對關愛患者考核分數的影響,并估計當某醫護人員的醫護專業知識考核分數為![]() 分時,他的關愛患者考核分數(精確到
分時,他的關愛患者考核分數(精確到![]() ).
).
參考公式及數據:回歸直線方程![]() 中斜率和截距的最小二乘法估計公式分別為
中斜率和截距的最小二乘法估計公式分別為
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現需要設計一個倉庫,由上下兩部分組成,上部的形狀是正四棱錐![]() ,下部的形狀是正四棱柱
,下部的形狀是正四棱柱![]() (如圖所示),并要求正四棱柱的高
(如圖所示),并要求正四棱柱的高![]() 是正四棱錐的高
是正四棱錐的高![]() 的4倍.
的4倍.

(1)若![]() ,
,![]() ,則倉庫的容積是多少?
,則倉庫的容積是多少?
(2)若正四棱錐的側棱長為![]() ,當
,當![]() 為多少時,下部的正四棱柱側面積最大,最大面積是多少?
為多少時,下部的正四棱柱側面積最大,最大面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com