
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,試討論函數(shù)
時,試討論函數(shù)![]() 的單調(diào)性,并求出函數(shù)
的單調(diào)性,并求出函數(shù)![]() 的極值;
的極值;
(2)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)①當![]() 時,
時, ![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增, ![]() 無極值,②當
無極值,②當![]() 時,
時, ![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減, ![]() 的極大值
的極大值![]() ,
, ![]() 無極小值(2)
無極小值(2)![]()
【解析】
(1)求出導數(shù),分![]() ,
,![]() 兩類討論求函數(shù)的單調(diào)區(qū)間及極值(2)原不等式恒成立轉(zhuǎn)化為
兩類討論求函數(shù)的單調(diào)區(qū)間及極值(2)原不等式恒成立轉(zhuǎn)化為![]() 恒成立,對
恒成立,對![]() 求導數(shù),分
求導數(shù),分![]() ,
,![]() 兩種情況討論,求出最小值
兩種情況討論,求出最小值![]() ,可得
,可得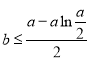 ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)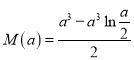 ,利用導數(shù)求最大值即可.
,利用導數(shù)求最大值即可.
(1)![]()
①當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
![]() 在
在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() 無極值
無極值
②當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
當![]() 時,
時,![]() 取得極大值
取得極大值![]() ,且
,且![]() 無極小值
無極小值
(2)![]() ,
,![]() .
.
若![]() ,由
,由![]() 知
知![]() ,取
,取![]() ,使得
,使得![]() ,
,
則![]() ,而
,而![]() ,
,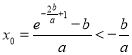
所以![]() ,所以
,所以![]() ,與
,與![]() 矛盾
矛盾
故![]() ,且
,且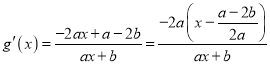 ,
,
故![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
因此![]() ,故
,故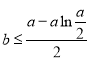
所以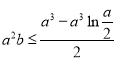
記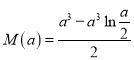 ,則
,則![]() ,則
,則![]() 在
在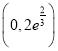 上單調(diào)遞增,在
上單調(diào)遞增,在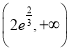 上單調(diào)遞減,因此
上單調(diào)遞減,因此 ,
,
所以當![]() ,
,![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業(yè)考試導與練系列答案
初中學業(yè)考試導與練系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 有極值,且導函數(shù)
有極值,且導函數(shù)![]() 的極值點是
的極值點是![]() 的零點,給出命題:①
的零點,給出命題:①![]() ;②若
;②若![]() ,則存在
,則存在![]() ,使得
,使得![]() ;③若
;③若![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,則
,則![]() ;④若
;④若![]() ,且
,且![]() 是曲線
是曲線![]() ,
,![]() 的一條切線,則
的一條切線,則![]() 的取值范圍是
的取值范圍是![]() ;則以上命題正確序號是______.
;則以上命題正確序號是______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年1月3日嫦娥四號探測器成功實現(xiàn)人類歷史上首次月球背面軟著陸,我國航天事業(yè)取得又一重大成就,實現(xiàn)月球背面軟著陸需要解決的一個關鍵技術(shù)問題是地面與探測器的通訊聯(lián)系.為解決這個問題,發(fā)射了嫦娥四號中繼星“鵲橋”,鵲橋沿著圍繞地月拉格朗日![]() 點的軌道運行.
點的軌道運行.![]() 點是平衡點,位于地月連線的延長線上.設地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,
點是平衡點,位于地月連線的延長線上.設地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,![]() 點到月球的距離為r,根據(jù)牛頓運動定律和萬有引力定律,r滿足方程:
點到月球的距離為r,根據(jù)牛頓運動定律和萬有引力定律,r滿足方程:
![]() .
.
設![]() ,由于
,由于![]() 的值很小,因此在近似計算中
的值很小,因此在近似計算中![]() ,則r的近似值為
,則r的近似值為
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩班舉行數(shù)學知識競賽,參賽學生的競賽得分統(tǒng)計結(jié)果如下表:
班級 | 參賽人數(shù) | 平均數(shù) | 中位數(shù) | 眾數(shù) | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同學分析上表后得到如下結(jié)論:
①甲、乙兩班學生的平均成績相同;
②乙班優(yōu)秀的人數(shù)少于甲班優(yōu)秀的人數(shù)(競賽得分![]() 分為優(yōu)秀);
分為優(yōu)秀);
③甲、乙兩班成績?yōu)?/span>85分的學生人數(shù)比成績?yōu)槠渌档膶W生人數(shù)多;
④乙班成績波動比甲班小.
其中正確結(jié)論有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知某校甲、乙、丙三個興趣小組的學生人數(shù)分別為36,24,12.現(xiàn)采用分層抽樣的方法從中抽取6人,進行睡眠質(zhì)量的調(diào)查.
(1)應從甲、乙、丙三個興趣小組的學生中分別抽取多少人?
(2)設抽出的6人分別用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示,現(xiàn)從6人中隨機抽取2人做進一步的身體檢查.
表示,現(xiàn)從6人中隨機抽取2人做進一步的身體檢查.
(i)試用所給字母列出所有可能的抽取結(jié)果;
(ii)設![]() 為事件“抽取的2人來自同一興趣小組”,求事件
為事件“抽取的2人來自同一興趣小組”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,過拋物線![]() 上一點
上一點![]() ,作兩條直線分別交拋物線于
,作兩條直線分別交拋物線于![]() ,
,![]() ,當
,當![]() 與
與![]() 的斜率存在且傾斜角互補時:
的斜率存在且傾斜角互補時:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 時,求
時,求![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
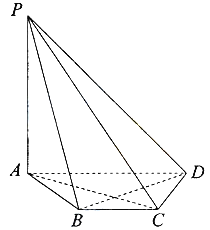
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)證明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直線PD與平面PAC所成的角為30°,求四棱錐P-ABCD的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某同學大學畢業(yè)后,決定利用所學專業(yè)進行自主創(chuàng)業(yè),經(jīng)過市場調(diào)查,生產(chǎn)一小型電子產(chǎn)品需投入固定成本2萬元,每生產(chǎn)![]() 萬件,需另投入流動成本
萬件,需另投入流動成本![]() 萬元,當年產(chǎn)量小于
萬元,當年產(chǎn)量小于![]() 萬件時,
萬件時,![]() (萬元);當年產(chǎn)量不小于7萬件時,
(萬元);當年產(chǎn)量不小于7萬件時,![]() (萬元).已知每件產(chǎn)品售價為6元,假若該同學生產(chǎn)的商品當年能全部售完.
(萬元).已知每件產(chǎn)品售價為6元,假若該同學生產(chǎn)的商品當年能全部售完.
(1)寫出年利潤![]() (萬年)關于年產(chǎn)量
(萬年)關于年產(chǎn)量![]() (萬件)的函數(shù)解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(萬件)的函數(shù)解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(2)當年產(chǎn)量約為多少萬件時,該同學的這一產(chǎn)品所獲年利潤最大?最大年利潤是多少?
(取![]() ).
).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com