，這個函數(shù)后來被稱為狄利克雷函數(shù)。下面對此函數(shù)性質的描述中不正確的是：（ ）| A．它沒有單調性 | B．它是周期函數(shù)，且沒有最小正周期 |
| C．它是偶函數(shù) | D．它有函數(shù)圖像 |
科目：高中數(shù)學 來源：不詳 題型：解答題
米，寬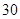
米的長方形體育館．按照建筑要求，每隔
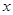米（
，
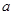為正常數(shù)）需打建一個樁位，每個樁位需花費
萬元（樁位視為一點且打在長方形的邊上），樁位之間的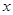米墻面需花
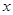萬元，在不計地板和天花板的情況下，當為何值時，所需總費用最少？查看答案和解析>>
科目：高中數(shù)學 來源：不詳 題型：單選題
是定義在正整數(shù)集上的函數(shù),且滿足:“當
成立時，總可推出
成立”，那么，下列命題總成立的是（ ）A．若 成立，則 成立 |
B．若 成立，則當 時，均有成立 |
C．若 成立，則 成立 |
D．若 成立，則當 時，均有成立 |
查看答案和解析>>
科目：高中數(shù)學 來源：不詳 題型：解答題
（萬元）的關系，有經(jīng)驗公式
，今有3萬元資金投入經(jīng)營甲、乙兩種商品，對甲、乙兩種商品的資金投入應分別為多少時，才能獲得最大利潤？查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
上可導的任意函數(shù)
,若滿足
,則必有（ ）
,Q=
,則下列對應中不是從P到Q的映射的是（ ）
是定義在R上的可導函數(shù)，且對任意的
滿足
，則對任意實數(shù)
，下面結論正確的是 （ ）
，若
，則
______．
______．
，則
的表達式為（ ）
